题目内容
9.计算:(1)已知x-2的平方根是±4,2x-y+12的立方根是4,求(x-y)x+y的值;
(2)在Rt△ABC中,∠C=90°,若c=10cm,a:b=3:4,求△ABC的周长.
分析 (1)根据平方根的性质和立方根的性质得出x-2=16,2x-y+12=64,求出x和y的值,再代入计算即可;
(2)设a=3xcm,b=4xcm,由勾股定理得出方程,解方程求出x,得出a和b,即可得出结果.
解答 解:(1)∵x-2的平方根是±4,2x-y+12的立方根是4,
∴x-2=16,2x-y+12=64,
∴x=18,y=-16,
∴(x-y)x+y=342=1156;
(2)设a=3xcm,b=4xcm,
∵∠C=90°,
∴(3x)2+(4x)2=102,
解得:x=2,
∴a=6,b=8,
∴△ABC的周长=a+b+c=6+8+10=24(cm).
点评 本题考查了平方根和立方根的性质、勾股定理、三角形周长的计算;熟练掌握平方根和立方根的性质以及勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
 如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )
如图,四边形ABCD中,AB=AC=AD,∠CBD=23°,则∠CAD为( )| A. | 47° | B. | 46° | C. | 45° | D. | 44° |
4.若|x|=|y|,那么x与y之间的关系是( )
| A. | 相等 | B. | 互为相反数 | ||
| C. | 相等或互为相反数 | D. | 无法判断 |
19.下面结论错误的是( )
| A. | 方程x2+4x+5=0,则x1+x2=-4,x1x2=5 | |
| B. | 方程2x2-3x+m=0有实根,则m≤$\frac{9}{8}$ | |
| C. | 方程x2-8x+1=0可配方得(x-4)2=15 | |
| D. | 方程x2+x-1=0两根x1=$\frac{{-1+\sqrt{5}}}{2}$,x2=$\frac{{-1-\sqrt{5}}}{2}$ |
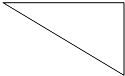 小芳想在墙壁上钉一个三角架(如图),其中两直角边长度之比为3:2,斜边长$\sqrt{520}$厘米,求两直角边的长度.
小芳想在墙壁上钉一个三角架(如图),其中两直角边长度之比为3:2,斜边长$\sqrt{520}$厘米,求两直角边的长度.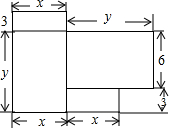 小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m).
小明家最近刚购置了一套商品房,如图是这套商品房的平面图(单位:m). 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.