��Ŀ����
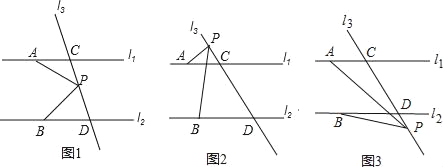
����Ŀ����ͼ1����ֱ֪��PQ��MN����A��ֱ��PQ�ϣ���C��D��ֱ��MN�ϣ�����AC��AD����PAC��50�㣬��ADC��30�㣬AEƽ�֡�PAD��CEƽ�֡�ACD��AE��CE�ཻ��E��
��1�����AEC�Ķ�����
��2������ͼ1�е��߶�AD��MN����ƽ�Ƶ�A1D1��ͼ2��ʾλ�ã���ʱA1Eƽ�֡�AA1D1��CEƽ�֡�ACD1��A1E��CE�ཻ��E����PAC��50�㣬��A1D1C��30�㣬���A1EC�Ķ�����
��3������ͼ1�е��߶�AD��MN����ƽ�Ƶ�A1D1��ͼ3��ʾλ�ã����������루2����ͬ�����ʱ��A1EC�Ķ�����

���𰸡���1����AEC��130�㣻��2����A1EC��130�㣻��3����A1EC��40�㣮
��������
(1)��ֱ��PQ��MN����ADC=��QAD=30�����ɵ���PAD=150����������PAE=75�����ɵ���CAE=25��������PAC=��ACN�������ECA=25��������AEC=180����25����25����
(2)�������QA1D1=30������PA1D1=150�����������PA1E=��EA1D1=75�����������CAQ=130������ACN=50��������ƽ���߶������ACE=25�����������ı����ڽǺ����ʿ�����CEA1��
(3)����ƽ�������ʺͽ�ƽ���߶���������QA1E=��2=15������ACE=��ECN=��1=25����������CEA1=��1+��2������ô�.
(1)��ͼ1��ʾ��

��ֱ��PQ��MN����ADC��30�㣬
���ADC����QAD��30�㣬
���PAD��150�㣬
�ߡ�PAC��50�㣬AEƽ�֡�PAD��
���PAE��75�㣬
���CAE��25�㣬
�ɵá�PAC����ACN��50�㣬
��CEƽ�֡�ACD��
���ECA��25�㣬
���AEC��180�㩁25�㩁25�㣽130�㣻
(2)��ͼ2��ʾ��
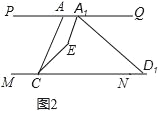
�ߡ�A1D1C��30�㣬�߶�AD��MN����ƽ�Ƶ�A1D1��PQ��MN��
���QA1D1��30�㣬
���PA1D1��150�㣬
��A1Eƽ�֡�AA1D1��
���PA1E����EA1D1��75�㣬
�ߡ�PAC��50�㣬PQ��MN��
���CAQ��130�㣬��ACN��50�㣬
��CEƽ�֡�ACD1��
���ACE��25�㣬
���CEA1��360�㩁25�㩁130�㩁75�㣽130�㣻
(3)��ͼ3��ʾ��
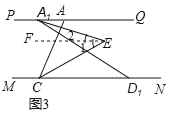
����E��FE��PQ��
�ߡ�A1D1C��30�㣬�߶�AD��MN����ƽ�Ƶ�A1D1��PQ��MN��
���QA1D1��30�㣬
��A1Eƽ�֡�AA1D1��
���QA1E����2��15�㣬
�ߡ�PAC��50�㣬PQ��MN��
���ACN��50�㣬
��CEƽ�֡�ACD1��
���ACE����ECN����1��25�㣬
���CEA1����1+��2��15��+25�㣽40�㣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
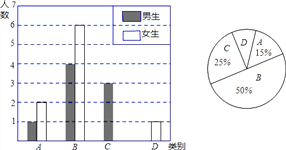
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij�������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μ�ʡ�����������ǽ��������β��ԣ����Գɼ����±�![]() ��λ����
�����![]() ��
��
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | |
�� | 10 | 9 | 8 | 8 | 10 | 9 |
�� | 10 | 10 | 8 | 10 | 7 | 9 |
���ݱ����е����ݣ��ɼ�����ס������˵�ƽ���ɼ�����9����
��1���ֱ����ס������β��Գɼ��ķ��
��2���������ݷ�����֪ʶ������Ϊѡ______����Ա������