Question

【题目】如图1，直线与轴交于点，交轴于点，直线与关于轴对称，交轴于点，

（1）求直线的解析式；

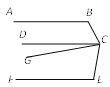
（2）过点在外作直线，过点作于点,过点作于点 ．求证：

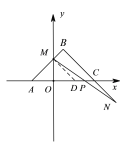
（3）如图2，如果沿轴向右平移，边交轴于点，点是的延长线上的一点，且，与轴交于点 ，在平移的过程中，的长度是否为定值，请说明理由．

Answer 1

【答案】（1）；（2）见解析；（3）是，理由见解析

【解析】

（1）先根据对称点的特点得出C点的坐标，然后利用待定系数法即可求出直线BC的解析式；

（2）首先通过等腰直角三角形的性质得出，然后证明，则有，最后利用即可证明；

（3）过点作交轴于点，首先根据平行线的性质和等腰三角形的性质得出，进而可证，则有，最后利用则可证明OP为定值．

解：（1），直线与关于轴对称，交轴于点，

∴点坐标是．

设直线解析式为，

把代入得：

解得：

∴直线BC的解析式为；

（2），

,和是全等的等腰直角三角形，

，

．

又，

，

，

．

在中

，

，

；

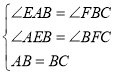
(3)为定值，理由如下：

过点作交轴于点，

，

．

，

，

，

．

，

．

，

．

在和中，

，

，

，

为定值．