Question

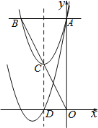
【题目】如图，抛物线与轴相交于点，与过点平行于轴的直线相交于点（点在第二象限），抛物线的顶点在直线上，且点为的中点，对称轴与轴相交于点，平移抛物线，使其经过点、，则平移后的抛物线的解析式为________．

Answer 1

【答案】

【解析】

先确定A（0，8），则表示出B点坐标（-b，8）（b＞0），利用点C为OB的中点可得到C（-b，4），根据抛物线的顶点坐标公式得到=4，解得b=4或b=-4（舍去），所以抛物线解析式为y=x2+4x+8=（x+2）2+4，则D（-2，0），然后设平移后的抛物线解析式为y=x2+mx+n，再把A点和D点坐标代入得到m、n的方程组，接着解方程组求出m、n即可．

解：当x=0时，y=x2+bx+8=8，则A（0，8），
∵AB∥x轴，
∴B点的纵坐标为8，
当y=8时，x2+bx+8=8，解得x1=0，x2=-b，
∴B（-b，8）（b＞0），
∵点C为OB的中点，

∴C（-b，4），

∵C点为抛物线的顶点，

∴=4，解得b=4或b=-4（舍去），
∴抛物线解析式为y=x2+4x+8=（x+2）2+4，
∴抛物线的对称轴为直线x=-2，
∴D（-2，0），
设平移后的抛物线解析式为y=x2+mx+n，
把A（0，8），D（-2，0）代入得，

，解得 ，

所以平移后的抛物线解析式为y=x2+6x+8．
故答案为y=x2+6x+8．