题目内容
1.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状如图.在平曲直角坐标系中两条抛物线关于y轴对称,AE∥x轴.AB=4cm.最低点C在x轴上,CH=1cm,BD=2cm,求右轮廓线DFE所在抛物线的函数解析式.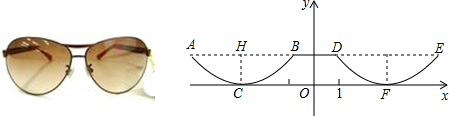
分析 利用B、D关于y轴对称,CH=1cm,BD=2cm可得到D点坐标为(1,1),由AB=4cm,最低点C在x轴上,则AB关于直线CH对称,可得到左边抛物线的顶点C的坐标为(-3,0),于是得到右边抛物线的顶点F的坐标为(3,0),然后设顶点式利用待定系数法求抛物线的解析式.
解答 解:∵高CH=1cm,BD=2cm,
而B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(-3,0),
∴右边抛物线的顶点F的坐标为(3,0),
设右边抛物线的解析式为y=a(x-3)2,
把D(1,1)代入得1=a×(1-3)2,解得a=$\frac{1}{4}$,
故右边抛物线的解析式为y=$\frac{1}{4}$(x-3)2.
点评 本题考查了二次函数的应用:利用实际问题中的数量关系与直角坐标系中线段对应起来,再确定某些点的坐标,然后利用待定系数法确定抛物线的解析式,再利用抛物线的性质解决问题.

练习册系列答案
相关题目
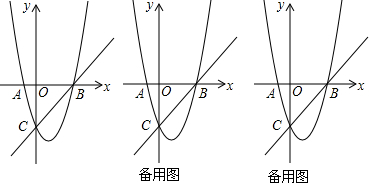
6.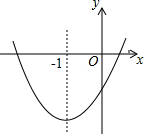 已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
①abc>0;②b=2a;③4ac-b2<0;④a+b+c<0;⑤4a+c<2b;⑥8a+c>0.
其中正确的个数是( )
 已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:
已知二次函数y=ax2+bx+c的图象如图所示(虚线部分是对称轴);则下列结论:①abc>0;②b=2a;③4ac-b2<0;④a+b+c<0;⑤4a+c<2b;⑥8a+c>0.
其中正确的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
13.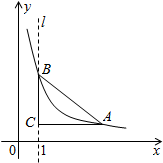 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=2.将BC边在直线l上滑动,使A、B在函数$y=\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=2.将BC边在直线l上滑动,使A、B在函数$y=\frac{k}{x}$的图象上.那么k的值是( )
 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=2.将BC边在直线l上滑动,使A、B在函数$y=\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=2.将BC边在直线l上滑动,使A、B在函数$y=\frac{k}{x}$的图象上.那么k的值是( )| A. | $\frac{15}{4}$ | B. | 6 | C. | $\frac{5}{2}$ | D. | 3 |
10.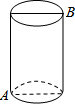 如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )
如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )
 如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )
如图,有一圆柱体,高9cm,底面周长24cm,在圆柱的下底面点A处有一蜘蛛,它想吃到上底面与点A相对的B处的苍蝇,需要爬行的最短路程是( )| A. | 9cm | B. | 10cm | C. | 12cm | D. | 15cm |
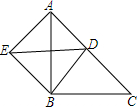 已知:如图,△ABC中,AB=BC,∠ABC=90°,点D在AC上,∠DBE=90°,BE=BD.求证:CD=AE.
已知:如图,△ABC中,AB=BC,∠ABC=90°,点D在AC上,∠DBE=90°,BE=BD.求证:CD=AE.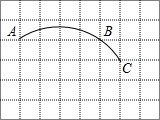 如图,边长为1的正方形网格中,一段圆弧经过网格的交点A,B,C.
如图,边长为1的正方形网格中,一段圆弧经过网格的交点A,B,C.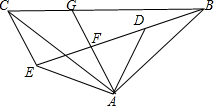 如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).
如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AG是∠DAE的平分线,分别交DE,BC于点F,G,连接CE,∠GAC=25°,下面结论正确的是①③④(填序号).