题目内容
2.直角三角形一直角边为5厘米、斜边为13厘米,那么斜边上的高是$\frac{60}{13}$cm2.分析 根据勾股定理求得其另一直角边的长,再根据面积公式即可求得其面积.
解答 解:∵直角三角形一直角边为5cm,斜边长为13cm,
∴另一直角边=$\sqrt{1{3}^{2}-{5}^{2}}$=12cm,
∴斜边上的高=$\frac{5×12}{13}$=$\frac{60}{13}$(cm2).
故答案为:$\frac{60}{13}$cm2.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若一个正方形的边长增加2cm,则面积相应增加了32cm2,那么这个正方形的边长为( )
| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
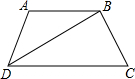 如图,在等腰梯形ABCD中,AB∥CD,AD=AB,BD⊥BC,则∠C=60°.
如图,在等腰梯形ABCD中,AB∥CD,AD=AB,BD⊥BC,则∠C=60°.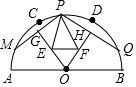 如图,点C、D是半径为6的半圆弧$\widehat{AB}$上的三等分点,O为圆心,M、Q分别是$\widehat{AC}$、$\widehat{DB}$上的动点,点P是$\widehat{CD}$上一点,且P不与C、D重合,连接PM、PQ,作OG⊥PM于G,OH⊥PQ于H,点E、F分别在线段OG、OH上的任意两点,连接PE、PF,则△PEF周长的最小值为( )
如图,点C、D是半径为6的半圆弧$\widehat{AB}$上的三等分点,O为圆心,M、Q分别是$\widehat{AC}$、$\widehat{DB}$上的动点,点P是$\widehat{CD}$上一点,且P不与C、D重合,连接PM、PQ,作OG⊥PM于G,OH⊥PQ于H,点E、F分别在线段OG、OH上的任意两点,连接PE、PF,则△PEF周长的最小值为( )