题目内容
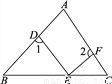
把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
【答案】BF⊥AE,理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD,CA=CB,∠ACE=∠BCD=90°,∴△BCD≌△ACE,∴BD=AE,∠CBD=∠CAE,∵∠CAE+∠AEC=90°,∴∠CBD+∠AEC=90°,∴∠BFE=90°,即BD⊥AE.
【题型】解答题
【结束】
24
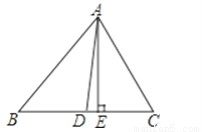
在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目


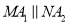 ,则
,则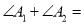 _________.
_________.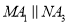 ,则
,则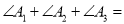 ___________.
___________.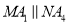 ,则
,则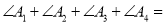 ___________.
___________.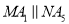 ,则
,则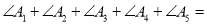 ___________.
___________.




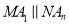 ,则
,则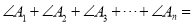 ______________.
______________. ,
,  和
和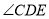 的平分线相交于
的平分线相交于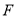 ,
, 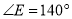 ,求
,求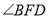 的度数.
的度数.
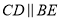 ,则
,则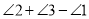 的度数等于( )
的度数等于( )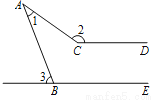
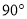 B.
B. 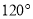 C.
C. 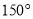 D.
D.