题目内容
 如下图,在等腰梯形ABCD中,AB∥CD,∠D=45°,AB=1,CD=3,BE∥AD交CD于E,则△BCE的周长l为
如下图,在等腰梯形ABCD中,AB∥CD,∠D=45°,AB=1,CD=3,BE∥AD交CD于E,则△BCE的周长l为考点:等腰梯形的性质,勾股定理的应用,平行四边形的判定与性质
专题:计算题
分析:首先根据等腰梯形的性质可得∠D=∠C=45°,进而得到∠EBC=90°,然后证明四边形ABED是平行四边形,可得AB=DE=1,再得EC=2,然后再根据勾股定理可得BE长,进而得到△BCE的周长.
解答:解:∵梯形ABCD是等腰梯形,
∴∠D=∠C=45°,
∵EB∥AD,
∴∠BEC=45°,
∴∠EBC=90°,
∵AB∥CD,BE∥AD,
∴四边形ABED是平行四边形,
∴AB=DE=1,
∵CD=3,
∴EC=3-1=2,
∵EB2+CB2=EC2,
∴EB=BC=
,
∴△BCE的周长为:2+2
,
故答案为:2+2
.
∴∠D=∠C=45°,
∵EB∥AD,
∴∠BEC=45°,
∴∠EBC=90°,
∵AB∥CD,BE∥AD,
∴四边形ABED是平行四边形,
∴AB=DE=1,
∵CD=3,
∴EC=3-1=2,
∵EB2+CB2=EC2,
∴EB=BC=
| 2 |
∴△BCE的周长为:2+2
| 2 |
故答案为:2+2
| 2 |
点评:此题主要考查了等腰梯形的性质,以及平行四边形的判定和性质,勾股定理的应用,关键是掌握等腰梯形同一底上的两个角相等.

练习册系列答案
相关题目
某事测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是( )
| A、50和50 |
| B、50和40 |
| C、40和50 |
| D、40和40 |
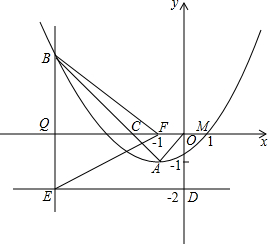 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).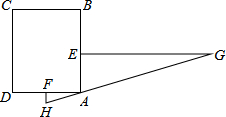 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=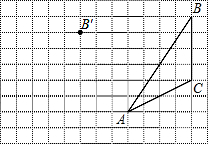 画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.