题目内容
6.先化简,再求值:$\frac{{x}^{2}-2x}{{x}^{2}-4x+4}$÷(x+3+$\frac{9}{x-3}$)-$\frac{1}{x}$,其中x=-2sin30°.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,求出x的值代入计算即可求出值.
解答 解:原式=$\frac{x(x-2)}{(x-2)^{2}}$•$\frac{x-3}{{x}^{2}}$-$\frac{1}{x}$=$\frac{x-3}{x(x-2)}$-$\frac{1}{x}$=$\frac{x-3-x+2}{x(x-2)}$=-$\frac{1}{x(x-2)}$,
当x=-2sin30°=-2×$\frac{1}{2}$=-1时,原式=-$\frac{1}{3}$.
点评 此题考查了分式的化简求值,以及特殊角的三角函数值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.观察下列标志,从图案看既是轴对称图形又是中心对称图形的有( )


| A. | 1个 | B. | 2 个 | C. | 3 个 | D. | 4个 |
1.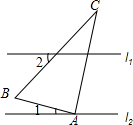 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
 如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,含60°角的直角三角板ABC的直角顶点A在直线l2上,且∠ABC=60°,∠1=45°,则∠2的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
18.在平面直角坐标系中,点P(3,-x2-1)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.在下列各对数值中,是方程2x+3y=-6的解的一组数值是( )
| A. | $\left\{\begin{array}{l}x=0\\ y=2\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=-3\\ y=0\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-3\\ y=-4\end{array}\right.$ |
 如图,在平移三角尺画平行线的过程中,理由是同位角相等,两直线平行.
如图,在平移三角尺画平行线的过程中,理由是同位角相等,两直线平行.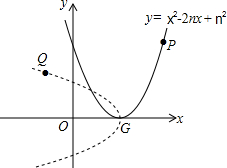 如图,已知抛物线y=x2-2nx+n2(n为常数,n>0),它的顶点为G,点P为抛物线右侧上任一点(不与G重合).
如图,已知抛物线y=x2-2nx+n2(n为常数,n>0),它的顶点为G,点P为抛物线右侧上任一点(不与G重合).