题目内容
17.解方程:(1)$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$
(2)$\frac{x}{x-2}$-$\frac{8}{{x}^{2}-4}$=1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:x-3+x-2=-3,
解得:x=1,
经检验x=1是分式方程的解;
(2)去分母得:x2+2x-8=x2-4,
解得:x=2,
经检验x=2是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.九张同样的卡片分别写有数字-5,-3,-2,-1,0,1,2,3,6,任意抽取一张,所抽卡片上数字的绝对值小于2的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
8.下列各式中,不是二次根式的是( )
| A. | $\sqrt{45}$ | B. | $\sqrt{-3}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\sqrt{\frac{2}{3}}$ |
7.下列运算中,正确的是( )
| A. | 3a2-a2=2 | B. | (-a2b)3=a6b3 | C. | a3•a6=a9 | D. | (2a2)2=2a4 |
 计算图中梯形的面积.
计算图中梯形的面积.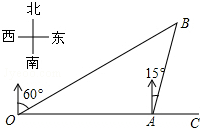 如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为2$\sqrt{2}$km.
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为2$\sqrt{2}$km.