题目内容
7.先化简,再求值:($\frac{1}{x-y}$-$\frac{1}{x+y}$)÷$\frac{2y}{{x}^{2}-2xy+{y}^{2}}$,x=$\sqrt{6}$+1,y=$\sqrt{6}$-1.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=$\frac{x+y-x+y}{(x+y)(x-y)}$•$\frac{(x-y)^{2}}{2y}$=$\frac{2y}{(x+y)(x-y)}$•$\frac{(x-y)^{2}}{2y}$=$\frac{x-y}{x+y}$,
当x=$\sqrt{6}$+1,y=$\sqrt{6}$-1时,原式=$\frac{\sqrt{6}+1-\sqrt{6}+1}{(\sqrt{6}+1)(\sqrt{6}-1)}$=$\frac{2}{5}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
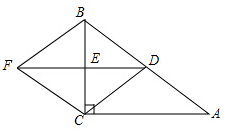 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC.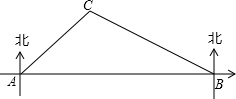 如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732)
如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=800m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}$≈1.732) 如图,在Rt△ABC中,∠C=90°,DE⊥AB垂足为点D,BC=BD,求证:DE=CE.(提示:连接BE)
如图,在Rt△ABC中,∠C=90°,DE⊥AB垂足为点D,BC=BD,求证:DE=CE.(提示:连接BE)