题目内容
如图,在平面直角坐标系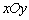 中,以点
中,以点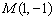 为圆心,以
为圆心,以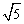 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经
的图象经
过点A、B、C,顶点为E.
(1)求此二次函数的表达式;
(2)设∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
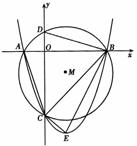
 解:(1)
解:(1)
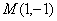 为圆心,半径为
为圆心,半径为
∴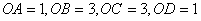
∴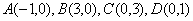
设二次函数的表达式为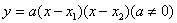
解得: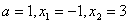
∴ 二次函数表达式为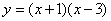
整理成一般式为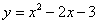
(2)过点E作EF⊥y轴于点F


∴可得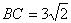
 点E为二次函数
点E为二次函数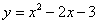 的顶点
的顶点
∴ 点E的坐标为
点E的坐标为
∴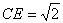

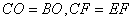
∴∠OCB=∠ECF=45º
∴∠BCE=90º
 在Rt△BCE中与Rt△BOD中,
在Rt△BCE中与Rt△BOD中,
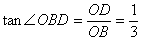 ,
,
∴∠CBE=∠OBD=b,
∴ sin(a-b)=sin(∠DBC-∠OBD)=sin∠OBC=
(3)显然 Rt△COA∽Rt△BCE,此时点P1(0,0)
过A作AP2⊥AC交y正半轴于P2,由Rt△CAP2 ∽Rt△BCE,得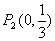
过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0)
故在坐标轴上存在三个点P1(0,0),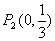 ,P3(9,0),使得以P、A、C为顶点的三角形与BCE相似
,P3(9,0),使得以P、A、C为顶点的三角形与BCE相似

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 C.
C. D.2
D.2 

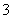
 ,弦AC=
,弦AC=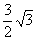 ,点P为半圆O上一点(不与点A、
,点P为半圆O上一点(不与点A、 .
. 
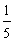 米,
米,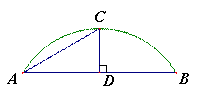
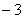 ,
,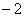 ,
,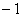 ,0,1,2,的小球,它们除数字不同外其余全部相同。现从盒子里随机取出一个小球,记下数字
,0,1,2,的小球,它们除数字不同外其余全部相同。现从盒子里随机取出一个小球,记下数字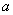 后不放回,再取出一个记下数字
后不放回,再取出一个记下数字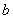 ,那么点
,那么点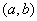 在抛物线
在抛物线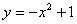 上的概率是( )
上的概率是( )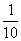 B.
B.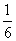 C.
C. D.
D.
 ,那么
,那么 ,
, 两个实数一定是( )
两个实数一定是( )