题目内容
如图:在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,AB=10,AC=6,求D到AB的距离.

 解:作DE⊥AB,垂足为E,
解:作DE⊥AB,垂足为E,
DE即为D到AB的距离
又∵∠C=90°,AD平分∠CAB,∴DE=DC
在△ABC中∵∠C=90°,AB=10,AC=6,∴BC=8,设CD=x,
则DE=CD=x,BD=8-x,∵∠DCE=∠DEA=90°,AD为公共边,
DE=CD ∴△ACD≌△AED (HL),∴AE= AC =6,∴BE=4,
在Rt△BED中,∵DE2+EB2=DB2,即x2+42=(8-x)2,
解得:x=3.
∴ D到AB的距离是3
(其它利用相似三角形的性质、三角函数定义、面积法相应给分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B重合),分别连接ED,EC,可以把
B重合),分别连接ED,EC,可以把 CD的边AB上的相似点,并说明理由;
CD的边AB上的相似点,并说明理由;
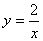 的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC
的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC 的面积记为S,则
的面积记为S,则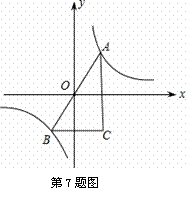
 xkb1.com
xkb1.com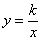 的图象如图所示,以下结论:①常数
的图象如图所示,以下结论:①常数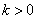 ;②当
;②当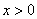 时,函数值
时,函数值 ;③
;③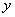 随
随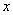 的增大而减小;④若点
的增大而减小;④若点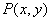 在此函数图象上,则点
在此函数图象上,则点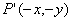 也在此函数图象上.其中正确的是 ( )
也在此函数图象上.其中正确的是 ( ) C.①②④ D.②③④
C.①②④ D.②③④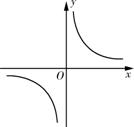
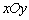 中,以点
中,以点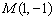 为圆心,以
为圆心,以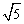 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经
的图象经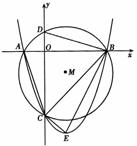
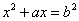 (a>0,b>0)的方程的图解法是:以
(a>0,b>0)的方程的图解法是:以 和b为两直角边做Rt△ABC,再在斜边上截取BD=
和b为两直角边做Rt△ABC,再在斜边上截取BD=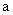 和线段b,作出方程的解。
和线段b,作出方程的解。