题目内容
16. 如图,抛物线y=mx2-4mx的图象于x轴交于点O,A,已知直线l的解析式为y=kx(k<0),点A关于l的对称点为点B,
如图,抛物线y=mx2-4mx的图象于x轴交于点O,A,已知直线l的解析式为y=kx(k<0),点A关于l的对称点为点B,(1)填空:点A的坐标是(4,0);
(2)求点B的坐标(用含k的代数式表示);
(3)若点B在抛物线上,点P在此抛物线的对称轴上,且四边形AOBP为平行四边形,求此抛物线的函数解析式.
分析 (1)令y=0,解方程即可;
(2)设B(m,n),过点A垂直y=kx的直线的解析式为y=-$\frac{1}{k}$x+b,利用方程组求出解交点坐标,再利用中点坐标公式,列出方程组求出m、n即可解决问题;
(3)由题意可知点B的横坐标为-2,列出方程即可求解;
解答 解:(1)对于抛物线令y=0,则有mx2-4mx=0,解得x=0,或4,
∴A(4,0),
故答案为(4,3).
(2)设B(m,n),过点A垂直y=kx的直线的解析式为y=-$\frac{1}{k}$x+b,
把A(4,0)代入得到0=-$\frac{4}{k}$+b,
∴b=$\frac{4}{k}$,
∴y=-$\frac{1}{k}$x+$\frac{4}{k}$,
由$\left\{\begin{array}{l}{y=kx}\\{y=-\frac{1}{k}x+\frac{4}{k}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{4}{1+{k}^{2}}}\\{y=\frac{4k}{1+{k}^{2}}}\end{array}\right.$,
∵A、B关于y=kx对称,
∴$\left\{\begin{array}{l}{\frac{m+4}{2}=\frac{4}{1+{k}^{2}}}\\{\frac{n+0}{2}=\frac{4k}{1+{k}^{2}}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{4-4{k}^{2}}{1+{k}^{2}}}\\{n=\frac{8k}{1+{k}^{2}}}\end{array}\right.$,
∴B($\frac{4-4{k}^{2}}{1+{k}^{2}}$,$\frac{8k}{1+{k}^{2}}$).
(3)如图,
∵四边形AOBP是平行四边形时,
∴OA=PB=4,
∵抛物线的对称轴x=2,
∴点B的横坐标为-2,
∴$\frac{4-4{k}^{2}}{1+{k}^{2}}$=-2,
∴k=±$\sqrt{3}$,
∵k<0,
∴k=-$\sqrt{3}$,
∴B(-2,-2$\sqrt{3}$),
把B(-2,-2$\sqrt{3}$)代入y=mx2-4mx得到,-2$\sqrt{3}$=4m+8m,
∴m=-$\frac{\sqrt{3}}{6}$,
∴抛物线的解析式为y=-$\frac{\sqrt{3}}{6}$x2+$\frac{2\sqrt{3}}{3}$x.
点评 本题考查二次函数综合题、一次函数的应用.两直线垂直的条件,中点坐标公式,二次一次方程组.平行四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会构建一次函数利用方程组求交点坐标,属于中考压轴题.

 走进文言文系列答案
走进文言文系列答案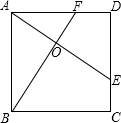 如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF中正确的有( )
如图,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:①AE=BF;②AE⊥BF;③AO=OE;④∠CEA=∠DFB;⑤S△AOB=S四边形DEOF中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| 等级 | 频数 | 频率 |
| 一等奖 | a | 0.1 |
| 二等奖 | 10 | 0.2 |
| 三等奖 | b | 0.4 |
| 优秀奖 | 15 | 0.3 |