题目内容
2. 如图,∠A=50°,∠B=35°,∠C=25°,求∠BDC的度数(提示:过A作射线AD)
如图,∠A=50°,∠B=35°,∠C=25°,求∠BDC的度数(提示:过A作射线AD)
分析 首先延长AD到E,根据三角形外角的性质可得∠BDE=∠BAD+∠B,再次利用三角形外角的性质可得∠EDC=∠CAD+∠C.
解答 解:延长AD到点E,
∴∠BDE=∠BAD+∠B,∠EDC=∠CAD+∠C,
∵∠A=50°,∠B=35°,∠C=25°,
∴∠BDC=∠BDE+∠CAD=50°+35°+25°=110°.
点评 此题主要考查了三角形外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
12.在下列各数中,最小的数是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 0 |
11.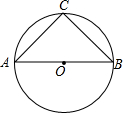 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
 若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )
若等腰直角三角形的外接圆半径的长为2,则等腰直角三角形的直角边长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
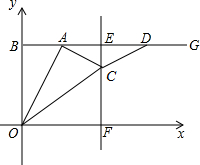 如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.
如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥x轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与x轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为t.