题目内容
如图5216，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝AC.
(1)求证：PA是⊙O的切线；
(2)若PD＝
，求⊙O的直径长．
(1)证明：连接OA，
∵∠B＝60°，∴∠AOC＝2∠B＝120°.
又∵OA＝OC，∴∠OAC＝∠OCA＝30°，
又∵AP＝AC，∴∠P＝∠ACP＝30°.
∴∠OAP＝∠AOC－∠P＝90°，∴OA⊥PA.
∴PA是⊙O的切线．
(2)在Rt△OAP中，∵∠P＝30°，
∴PO＝2OA＝OD＋PD.
又∵OA＝OD，∴PD＝OA.
∵PD＝，∴2OA＝2PD＝2 .
∴⊙O的直径为2 .
练习册系列答案
阅读快车系列答案
相关题目
轴正半轴上的一个定点，点B是反比例函数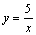
图像（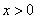
）上的一个动点，当点B的横坐标逐渐增大时，
A．逐渐增大 B．不变 C．逐渐减小 D．先减小后增大
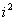=-1,这个数i叫做虚数单位。那么和我们所学的实数对应起来就叫做复数，表示为
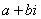（a,b为实数），a叫这个复数的实部，b叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似。
.
=_________, 
=____________.
； 
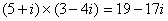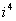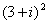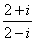化简成
D．－