题目内容
18.若x,y,a,b满足关系式$\sqrt{3x-6}$+$\sqrt{3y-7}$=$\sqrt{a+b-2011}$•$\sqrt{2011-a-b}$,试求x,y的值.分析 首先根据二次根式中的被开方数是非负数,可得$\left\{\begin{array}{l}{a+b-2011≥0}\\{2011-a-b≥0}\end{array}\right.$,解得a+b=2011,所以$\sqrt{3x-6}$+$\sqrt{3y-7}$=0,然后根据$\left\{\begin{array}{l}{3x-6=0}\\{3y-7=0}\end{array}\right.$,求出x,y的值各是多少即可.
解答 解:∵二次根式中的被开方数是非负数,
∴$\left\{\begin{array}{l}{a+b-2011≥0}\\{2011-a-b≥0}\end{array}\right.$,
∴a+b=2011,
∴a+b-2011=2011-a-b=0,
∴$\sqrt{3x-6}$+$\sqrt{3y-7}$=0,
∴$\left\{\begin{array}{l}{3x-6=0}\\{3y-7=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=2\frac{1}{3}}\end{array}\right.$
即x的值是2,y的值是2$\frac{1}{3}$.
点评 (1)此题主要考查了二次根式有意义的条件,要熟练掌握,解答此题的关键是要明确:二次根式中的被开方数是非负数.
(2)此题还考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:①被开方数a是非负数;②算术平方根a本身是非负数.求一个非负数的算术平方根与求一个数的平方互为逆运算,在求一个非负数的算术平方根时,可以借助乘方运算来寻找.

练习册系列答案
相关题目
13.下列各式正确的是( )
| A. | (a-b)2=-(b-a)2 | B. | $\frac{1}{{x}^{3}}$=x-3 | C. | $\frac{{a}^{2}+1}{a+1}$=a+1 | D. | x6÷x2=x3 |
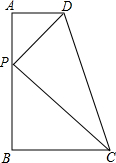 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=5$\sqrt{2}$,点P在线段AB上.若△PCD是以点P为直角顶点的直角三角形,则AP=1或6.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=5$\sqrt{2}$,点P在线段AB上.若△PCD是以点P为直角顶点的直角三角形,则AP=1或6.