题目内容
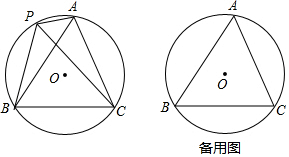
8．
如图，在Rt△ABC中，∠ACB=90°，以Rt△ABC的三边为边向外作正方形，其面积分别为S1，S2，S3，若S1=4，S2=8，则AB的长为（ ）| A． | 12 | B． | 4$\sqrt{5}$ | C． | 2$\sqrt{3}$ | D． | 2 |
分析 先利用正方形的面积公式分别求出正方形S1、S2的边长即AC、BC的长，在Rt△ABC中，已知AC、BC的长，利用勾股定理求斜边AB．
解答 解：
∵S1=4，
∴BC2=4，
∵S2=8，
∴AC2=8，
在Rt△ABC中，BC2+AC2=AB2，
故可得：AB=$\sqrt{4+8}$=2$\sqrt{3}$；
故选：C．
点评 本题考查了勾股定理的知识，根据图形得出S1=BC2，S2=AC2是解答本题的关键，另外要熟练勾股定理的运用．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
19．数6、-1、15、-3中，最小的数是（ ）
| A． | 6 | B． | -1 | C． | 15 | D． | -3 |
16．下列各组数中能作为直角三角形的三边长的是（ ）
| A． | 1，2，2 | B． | 2，3，4 | C． | $\sqrt{2}$a，$\sqrt{3}$a，a | D． | 4，5，6 |
3．
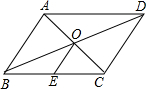如图，?ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）
如图，?ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）| A． | 3 cm | B． | 6 cm | C． | 9 cm | D． | 12 cm |
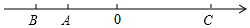如图，a、b、c分别是数轴上A、B、C所对应的实数．试化简$\sqrt{c^2}$+|a-b|+$\root{3}{（a+b）^{3}}$+|b-c|．