题目内容
1．
已知：如图，E、F为平行四边形ABCD对角线AC上两点，且AE=CF，连接DE、EB、BF、FD，求证：四边形DEBF为平行四边形．
分析 先连接BD，交AC于O，由于四边形ABCD是平行四边形，易知OB=OD，OA=OC，而AE=CF，根据等式性质易得OE=OF，再根据两组对角线互相平分的四边形是平行四边形可证之．
解答 
证明：连接BD，交AC于O，
∵四边形ABCD是平行四边形，
∴OB=OD，OA=OC，
∵AE=CF，
∴OA-AE=OC-CF，
∴OE=OF，
∴四边形BFDE是平行四边形．
点评 本题考查了平行四边形的判定和性质，解题的关键是作辅助线，使其中出现对角线相交的情况．
练习册系列答案
相关题目
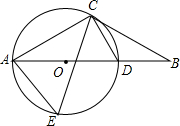如图，在△ABC中，AC=BC，∠CAB=30°，过点C作CD⊥AC交AB于点D，⊙O是△ACD的外接圆．
如图，长方体的底面是边长为1cm的正方形，高为3cm，如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，请利用侧面展开图计算所用细线最短需要多少5cm．
如图是边长为2的正方形ABCD，对角线为AC，△ABC以点A为中心，顺时针旋转45°得△AB′C′，则图中阴影部分的面积为4$\sqrt{2}$-4．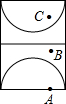
在某篮球比赛中，甲队队员A、B的位置如图所示，队员A抢到篮板球后，迅速将球抛向对方半场的点C处，队员B看到后同时快跑到点C处恰好接住了球，则如图中分别表示球、队员B离队员A的距离y（m）与队员A抛球后的时间x的关系的大致图象是（ ）
13．下面给出了四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是（ ）
| A． | 1：2：3：4 | B． | 2：2：3：3 | C． | 2；3：2：3 | D． | 2：3：3：2 |