题目内容
14.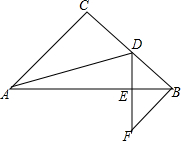 在△ABC中,AC=BC,∠C=90°,点D是BC的中点,DF⊥AB,交AB于E,交过点B平行于AC的直线于F.试说明CD=BF.
在△ABC中,AC=BC,∠C=90°,点D是BC的中点,DF⊥AB,交AB于E,交过点B平行于AC的直线于F.试说明CD=BF.
分析 求出∠CAD=∠BCF,∠CBF=∠ACD,证△ACD≌△CBF,推出CD=BF即可.
解答 证明:∵∠ACD=90°,CE⊥AD,
∴∠CED=90°,
∴∠CAD+∠CDA=90°,∠CDE+∠BCF=90°,
∴∠CAD=∠BCF,
∵BF∥AC,∠ACB=90°,
∴∠CBF=90°=∠ACD,
在△ACD和△CBF中
$\left\{\begin{array}{l}{∠ACD=∠CBF}\\{AC=BC}\\{∠CAD=∠BCF}\end{array}\right.$,
∴△ACD≌△CBF,
∴CD=BF,
∵D为BC的中点,
∴CD=BD,
∴BD=BF
点评 本题考查了全等三角形的性质和判定,关键是根据等腰直角三角形,等腰三角形性质的应用解答.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
2.下列各组线段中,能组成比例线段的是( )
| A. | 0.1,0.2,0.3,0.4 | B. | 0.2,0.8,12,30 | C. | 1,3,4,6 | D. | 12,16,45,60 |
9.下列方程中,是关于x的一元二次方程的是( )
| A. | x-$\frac{1}{x}$=1 | B. | (x+1)(x-1)=x(x+2) | C. | x2=0 | D. | x3+x2+2=0 |
3.若关于x的一元二次方程(m-2)x2+5x+m2-3m+2=0有一根为0,则另一根等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 5 |
 如图,抛物线y=(x-1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
如图,抛物线y=(x-1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.