题目内容
4. 如图,抛物线y=(x-1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
如图,抛物线y=(x-1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)点Q在x轴上,且∠ADQ=∠DAC,请直接写出点Q的坐标.
分析 (1)利用待定系数法即可求出n,利用对称性C、D关于对称轴对称即可求出点D坐标.
(2)A,P,D三点在同一直线上时△PAC的周长最小,求出直线AD的解析式即可解决问题.
(3)分两种情形①作DQ∥AC交x轴于点Q,此时∠DQA=∠DAC,满足条件.②设线段AD的垂直平分线交AC于E,直线DE与x的交点为Q′,此时∠Q′DA=′CAD,满足条件,分别求解即可.
解答 解:(1)把C(0,-3)代入y=(x-1)2+n,得,-3=(0-1)2+n,
解得n=-4,
∴抛物线的解析式为y=(x-1)2-4,
∴抛物线的对称轴为直线x=1,
∵点D与点C关于抛物线的对称轴对称,
∴点D的坐标为(2,-3).
(2)连接PA、PC、PD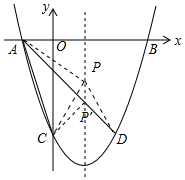
∵点D与点C关于抛物线的对称轴对称
∴PC=PD
∴AC+PA+PC=AC+PA+PD…(5分)
∵AC为定值,PA+PD≥AD
∴当PA+PC的值最小,即A,P,D三点在同一直线上时△PAC的周长最小,
由y=(x-1)2-4=0解得,x1=-1,x2=3,
∵A在B的左侧,∴A(-1,0),
由A,D两点坐标可求得直线AD的解析式为y=-x-1,
当x=1时,y=-x-1=-2,
∴当△PAC的周长最小时,点P的坐标为(1,-2),
(3)如图2中,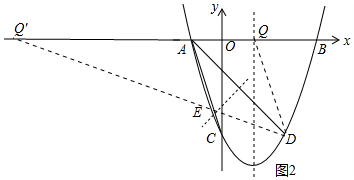
①作DQ∥AC交x轴于点Q,此时∠DQA=∠DAC,满足条件.
∵A(-1,0),C(0,-3),
∴直线AC的解析式为y=-3x-3,
∴直线QD的解析式为y=-3x+3,
令y=0得x=1,
∴Q(1,0).
②设线段AD的垂直平分线交AC于E,直线DE与x的交点为Q′,此时∠Q′DA=′CAD,满足条件,
∵直线AD的解析式为y=-x-1,
∴线段AD的中垂线是解析式为y=x-2,
由$\left\{\begin{array}{l}{y=x-2}\\{y=-3x-3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{1}{4}}\\{y=-\frac{9}{4}}\end{array}\right.$,
∴E(-$\frac{1}{4}$,-$\frac{9}{4}$),
∴直线DE的解析式为y=-$\frac{1}{3}$x-$\frac{7}{3}$,
令y=0得到x=-7,
∴Q′(-7,0).
综上所述,Q点坐标为(1,0)或(-7,0).
点评 本题考查二次函数综合题、一次函数、最小值问题、等腰三角形的性质、平行线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用对称解决最短问题,学会分类讨论的思想思考问题,属于中考压轴题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
| A. | -32+(-3)2=0 | B. | -32-32=0 | C. | -32-(-3)2=0 | D. | (-3)2+32=0 |
| A. | 2ab2 | B. | -3a2 | C. | ab | D. | $\frac{b{a}^{2}}{5}$ |
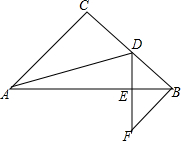 在△ABC中,AC=BC,∠C=90°,点D是BC的中点,DF⊥AB,交AB于E,交过点B平行于AC的直线于F.试说明CD=BF.
在△ABC中,AC=BC,∠C=90°,点D是BC的中点,DF⊥AB,交AB于E,交过点B平行于AC的直线于F.试说明CD=BF.