题目内容
1.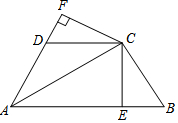 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.(1)求证:△BCE≌△DCF;
(2)直接写出线段AB、AD、DF的关系;
(3)若AB=15,AD=7,BC=5,求CE的长.
分析 (1)易证∠CFD=90°,∠CEB=90°,CE=CF,即可证明Rt△BCE≌Rt△DCF;
(2)由Rt△ACF≌Rt△ACE(HL),推出AF=AE,由Rt△BCE≌Rt△DCF,推出DF=BE,即可推出AB-AD=(AE+EB)-(AF-DF)=2DF,
(3)利用(2)中结论,求出EB,在Rt△EBC中,利用勾股定理即可解决问题.
解答 (1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴∠CFD=90°,∠CEB=90°,CE=CF,
在Rt△BCE和Rt△DCF中,
$\left\{\begin{array}{l}{CE=CF}\\{BC=CD}\end{array}\right.$,
∴Rt△BCE≌Rt△DCF(HL);
(2)解:结论:AB-AD=2DF,
理由:∵AC平分∠BAD,CF⊥AF,CE⊥AE,
∴CF=CE,
在Rt△ACF和Rt△ACE中,
$\left\{\begin{array}{l}{AC=AC}\\{CF=CE}\end{array}\right.$,
∴Rt△ACF≌Rt△ACE(HL),
∴AF=AE,
∵Rt△BCE≌Rt△DCF,
∴DF=BE,
∴AB-AD=(AE+EB)-(AF-DF)=2DF,
(3)解:∵AB=15,AD=7,
∴2DF=AB-AD=8,
∴DF=EB=4,
在Rt△BCE中,CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∴EC=3.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证Rt△BCE≌Rt△DCF和Rt△ACF≌Rt△ACE是解题的关键.

练习册系列答案
相关题目
13.现有以下命题:
①平分弦的直径垂直平分弦,平分弦所对的弧;
②等弧所对的弦相等,所对的圆周角相等;
③边数相等的正多边形都相似;
④有一个角相等的两个等腰三角形相似.
正确的有( )
①平分弦的直径垂直平分弦,平分弦所对的弧;
②等弧所对的弦相等,所对的圆周角相等;
③边数相等的正多边形都相似;
④有一个角相等的两个等腰三角形相似.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.一股民上周末以每股27元价格买了1000股股票,表为本周内每日股票的涨跌情况(单位:元)
(1)星期四收盘时,每股多少元?
(2)本周内每股最高价,最低价分别是多少元?
(3)已知该股民买进股票时付了百分之零点一五的手续费,卖出时需付成交额百分之零点一五的手续费和百分之零点一的交易税,如果他一直观望到星期五才将股票全部卖出,请你算算他本周的收益如何.
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 涨跌(与前一交易日比较) | +4 | +4.5 | -1 | -2.5 | -4 |
(2)本周内每股最高价,最低价分别是多少元?
(3)已知该股民买进股票时付了百分之零点一五的手续费,卖出时需付成交额百分之零点一五的手续费和百分之零点一的交易税,如果他一直观望到星期五才将股票全部卖出,请你算算他本周的收益如何.
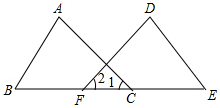 在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.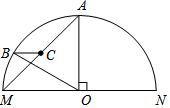 如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.
如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.