题目内容
16. 如图,函数y=-2x和y=ax+4的图象相交于A(m,3),则关于x的不等式0<ax+4<-2x的解集是-6<x<-$\frac{3}{2}$.
如图,函数y=-2x和y=ax+4的图象相交于A(m,3),则关于x的不等式0<ax+4<-2x的解集是-6<x<-$\frac{3}{2}$.
分析 先把A(m,3)代入y=-2x得到A(-$\frac{3}{2}$,3),再把A点坐标代入y=ax+4求出a,接着计算出直线y=ax+4与x轴的交点坐标,然后找出直线y=ax+4在x轴上方且在直线y=-2x的下方所对应的自变量的范围即可.
解答 解:当y=3时,-2x=3,解得x=-$\frac{3}{2}$,则两直线的交点A坐标为(-$\frac{3}{2}$,3),
把(-$\frac{3}{2}$,3)代入y=ax+4得-$\frac{3}{2}$a+4=3,解得a=$\frac{2}{3}$,
当y=0时,$\frac{2}{3}$x+4=0,解得x=-6,则直线y=ax+4与x轴的交点坐标为(-6,0),
所以当-6<x<-$\frac{3}{2}$时,0<ax+4<-2x.
故答案为-6<x<-$\frac{3}{2}$.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
 如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )
如图,若AB=AC,∠1=∠2,则下列条件不能使△ABD≌△ACE的是( )| A. | AE=AD | B. | ∠B=∠C | C. | ∠E=∠D | D. | BD=CE |
1.点P(-1,3)关于x轴对称的点的坐标是( )
| A. | (-1,-3) | B. | (1,-3) | C. | (1,3) | D. | (-3,1) |
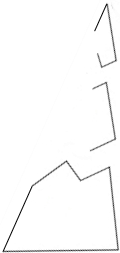 课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么?
课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么? 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.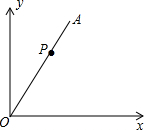 如图,P是∠AOx的边OA上的一点,且点P的坐标为(1,$\sqrt{3}$),则∠AOx=60度.
如图,P是∠AOx的边OA上的一点,且点P的坐标为(1,$\sqrt{3}$),则∠AOx=60度.