题目内容
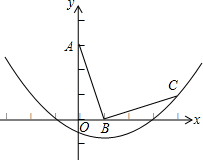 如图,在平面直角坐标系中,点A、B的坐标分别为(0,3)、(1,0),连接AB将线段AB绕点B旋转90°得到线段CB.抛物线y=
如图,在平面直角坐标系中,点A、B的坐标分别为(0,3)、(1,0),连接AB将线段AB绕点B旋转90°得到线段CB.抛物线y=| 1 |
| 5 |
| 3 |
| 5 |
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若将线段AB向右平移,使点B恰好落在抛物线上,求线段AB扫过的面积.
考点:二次函数图象与几何变换
专题:
分析:(1)如图,连接AC,利用勾股定理进行解答;
(2)把点C的坐标代入函数解析式,通过方程来求系数b的值;
(3)所扫过的部分平行四边形,根据平行四边形的面积公式进行解答.
(2)把点C的坐标代入函数解析式,通过方程来求系数b的值;
(3)所扫过的部分平行四边形,根据平行四边形的面积公式进行解答.
解答: 解:(1)如图,连接AC.
解:(1)如图,连接AC.
设C(x,y)(x、y>0).则
,
解得
.
故C(4,1).
(2)由(1)知,C(4,1).将其代入y=
x2+bx-
,得
×42+4b-
=1,
解得 b=-
.
则该函数的解析式为:y=
x2-
x-
.
(3)令y=0,则
x2-
x-
=0,整理,得
(x+1)(x-3)=0,
则x1=-1,x2=3,
故D(3,0).
∵B(1,0),
∴DB=2,
则S平行四边形ABDE=BD•OA=2×3=6,即线段AB扫过的面积是6.
 解:(1)如图,连接AC.
解:(1)如图,连接AC.设C(x,y)(x、y>0).则
|
解得
|
故C(4,1).
(2)由(1)知,C(4,1).将其代入y=
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
解得 b=-
| 2 |
| 5 |
则该函数的解析式为:y=
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
(3)令y=0,则
| 1 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
(x+1)(x-3)=0,
则x1=-1,x2=3,
故D(3,0).
∵B(1,0),
∴DB=2,
则S平行四边形ABDE=BD•OA=2×3=6,即线段AB扫过的面积是6.
点评:本题考查了二次函数图象与几何变换.此题利用待定系数法来求二次函数的解析式,这是中学阶段经常考核的知识点之一.

练习册系列答案
相关题目
若单项式-2a3-mb2与3abn-3的和仍为单项式,则m+n=( )
| A、6 | B、7 | C、8 | D、9 |
下列现象属于平移变换的是( )
| A、足球在草地上滚动 |
| B、钟摆的摆动 |
| C、传送带上,瓶装饮料的移动 |
| D、足球飞入球网中 |
若二次函数y=(m-1)xm2-m的开口向下,则m的值是( )
| A、2 | B、-1 |
| C、2或-1 | D、以上答案都不对 |
 如图,拦水坝的坡度i=1:
如图,拦水坝的坡度i=1: 如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限,则点B的对应点B′的坐标是
如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限,则点B的对应点B′的坐标是