��Ŀ����
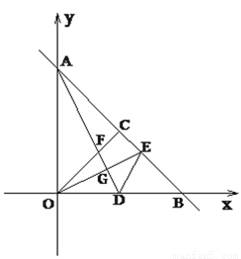
��ͼ,��ƽ��ֱ������ϵ��,ֱ��AB��������ֱ���A��B����,��֪��A������Ϊ��0��8��,��B������Ϊ(8��0),OC��AD���ǡ�OAB������,OC��AD�ཻ�ڵ�F,OE��AD��G��AB��E.
(1)��C������Ϊ__________��
(2)��֤����AFO�ա�OEB��
(3)��֤����ADO����EDB
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ,��ƽ��ֱ������ϵ��,ֱ��AB��������ֱ���A��B����,��֪��A������Ϊ��0��8��,��B������Ϊ(8��0),OC��AD���ǡ�OAB������,OC��AD�ཻ�ڵ�F,OE��AD��G��AB��E.
(1)��C������Ϊ__________��
(2)��֤����AFO�ա�OEB��
(3)��֤����ADO����EDB
