题目内容
4.老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下: ×(-$\frac{1}{2}$xy)=3x2y-xy2+$\frac{1}{2}$xy
×(-$\frac{1}{2}$xy)=3x2y-xy2+$\frac{1}{2}$xy(1)求所捂的多项式;
(2)若x=$\frac{2}{3}$,y=$\frac{1}{2}$,求所捂多项式的值.
分析 (1)设多项式为A,则A=(3x2y-xy2+$\frac{1}{2}$xy)÷(-$\frac{1}{2}$xy)计算即可.
(2)把x=$\frac{2}{3}$,y=$\frac{1}{2}$代入多项式求值即可.
解答 解:(1)设多项式为A,
则A=(3x2y-xy2+$\frac{1}{2}$xy)÷(-$\frac{1}{2}$xy)=-6x+2y-1.
(2)∵x=$\frac{2}{3}$,y=$\frac{1}{2}$,
∴原式=-6×$\frac{2}{3}$+2×$\frac{1}{2}$-1=-4+1-1=-4.
点评 本题考查单项式乘多项式、多项式除以单项式的法则,解题的关键是利用乘法与除法是互为逆运算,把乘法转化为除法解决问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在等腰直角三角形所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形,这样的点一共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
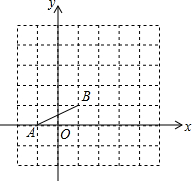 如图,已知A(-1,0),B(1,1),把线段AB平移,使点B移动到点D(3,4)处,这时点A移动到点C处.
如图,已知A(-1,0),B(1,1),把线段AB平移,使点B移动到点D(3,4)处,这时点A移动到点C处. 请找出图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.
请找出图中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有5个.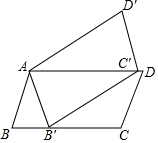 如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点),点B′恰好落在BC边上,则∠C=105°.
如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点),点B′恰好落在BC边上,则∠C=105°.