��Ŀ����
��ͼ���ڡ�ABC�У�AB=AC��DΪBC�е㣬��BAD=35�㣬���C�Ķ���Ϊ ��
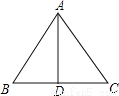
��ϰ��ϵ�д�
 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�
�����Ŀ
��Ŀ����
��ͼ���ڡ�ABC�У�AB=AC��DΪBC�е㣬��BAD=35�㣬���C�Ķ���Ϊ ��
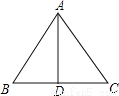
 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�