题目内容
 在梯形ABCD中,CD∥AB,∠DAB=∠B=30°,CD=2
在梯形ABCD中,CD∥AB,∠DAB=∠B=30°,CD=2| 3 |
| 3 |
(1)求y关于x的函数解析式,并写出定义域.
(2)如果四边形APCD的面积为3
| 3 |
考点:相似三角形的判定与性质,函数关系式,梯形
专题:
分析:(1)根据30°角的直角三角形的性质求得PF=
BP=
x,然后根据三角形面积公式即可求得y关于x的函数解析式.
(2)根据30°角的直角三角形的性质求得CE=
BC=
×4=2,然后根据S梯形ABCD=S四边形APCD+S△ABP得到关于x的方程,解方程即可求得BP的长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据30°角的直角三角形的性质求得CE=
| 1 |
| 2 |
| 1 |
| 2 |
解答: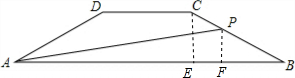 解:(1)如图,作PF⊥AB于F,
解:(1)如图,作PF⊥AB于F,
∵∠B=30°,
∴PF=
BP=
x,
∴△ABP的面积=
AB•PF,
即y=
×6
×
x=
x(0<x<4).
(2)作CE⊥AB于E,
∵∠B=30°,
∴CE=
BC=
×4=2,
∵S梯形ABCD=S四边形APCD+S△ABP,四边形APCD的面积为3
,
∴
(2
+6
)×2=3
+
x,
解得x=
,
∴BP的长为
.
 解:(1)如图,作PF⊥AB于F,
解:(1)如图,作PF⊥AB于F,∵∠B=30°,
∴PF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABP的面积=
| 1 |
| 2 |
即y=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
(2)作CE⊥AB于E,
∵∠B=30°,
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
∵S梯形ABCD=S四边形APCD+S△ABP,四边形APCD的面积为3
| 3 |
∴
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
3
| ||
| 2 |
解得x=
| 10 |
| 3 |
∴BP的长为
| 10 |
| 3 |
点评:本题考查了30°角的直角三角形的性质,三角形的面积以及梯形的面积,作出辅助线关键直角三角形是解题的关键.

练习册系列答案
相关题目
 已知,如图,AB∥DC,AC、BD交于O,且AC=BD,求证:OD=OC.
已知,如图,AB∥DC,AC、BD交于O,且AC=BD,求证:OD=OC. 如图,用数字表示的角中,哪些是同位角?哪些是内错角?哪些是同旁内角.
如图,用数字表示的角中,哪些是同位角?哪些是内错角?哪些是同旁内角. 2013年开始,国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.某日随机抽取25个城市检测点的研究性数据,并绘制成统计表和扇形统计图如下:
2013年开始,国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.某日随机抽取25个城市检测点的研究性数据,并绘制成统计表和扇形统计图如下: 已知:如图,函数y1=ax的图象与函数y2=
已知:如图,函数y1=ax的图象与函数y2=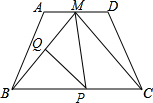 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5 如图,OA=OC,已知tan∠AOC=
如图,OA=OC,已知tan∠AOC= 如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=DE=EC.求证:
如图,在△ABC中,∠B=90°,点D、E在BC上,且AB=BD=DE=EC.求证: