Question

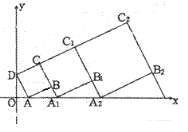
【题目】如图，平行于x轴的直线AC分别交抛物线 （x≥0）与 （x≥0）于B、C两点，过点C作y轴的平行线交y1于点D，直线DE∥AC，交y2于点E，则 = ．

Answer 1

【答案】
【解析】解：设A点坐标为(0,a),(a>0)，

则x2=a,解得x= ，

∴点B( ,a),

∴AB= .

∵ =a，

则x= ，

∴点C( ,a)，

∵CD∥y轴，

∴点D的横坐标与点C的横坐标相同为 ，

∴y1=( )2=5a，

∴点D的坐标为( ,5a).

∵DE∥AC，

∴点E的纵坐标为5a，

∴ =5a，

∴x=5 ，

∴点E的坐标为(5 ,5a)，

∴DE=5 － ，

∴ = .

故答案是： .

设A点坐标为(0,a)，根据已知过点C作y轴的平行线交y1于点D，可得出点A、B、C的纵坐标相等，就可分别表示出点B、C的坐标，利用勾股定理求出AB的长，而CD∥y轴，得出点D的横坐标与点C的横坐标相同，从而可以表示出点D的坐标，又有DE∥AC，则点D、E的纵坐标相等，可表示出点E的坐标，从而求出DE的长，即可求出结果。