题目内容
7.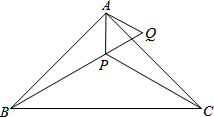 如图,Rt△ABC中,∠BAC=90°,AB=AC,点P是三角形△ABC内部一点,∠ABP=∠ACP,过点A作AQ∥PC交BP的延长线于Q.
如图,Rt△ABC中,∠BAC=90°,AB=AC,点P是三角形△ABC内部一点,∠ABP=∠ACP,过点A作AQ∥PC交BP的延长线于Q.(1)求证:AP平分∠BAC;
(2)若BQ=PB+PA,点M在BC边上,△PBM是等腰三角形,求∠BMP的度数.
分析 (1)先证明∠PBC=∠PCB得到PB=PC,然后证明△ABP≌△ACP得到∠BAP=∠CAP即可;
(2)易得PA=PQ,利用等腰三角形的性质得∠PQA=∠PAQ=∠PAC+∠2,再根据平行线的性质得∠1=∠2,设∠1=∠3=x,则∠PQA=∠PAQ=30°+x,利用三角形内角和和三角形外角性质得180°-2(30°+x)=x+30°,解得x=30°,则∠PBC=15°,然后分类讨论:利用等腰三角形的性质和三角形内角和,当MP=MB或PM=PB或BM=BP时∠BMP的度数.
解答 (1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠ABP=∠ACP,
∴∠PBC=∠PCB,
∴PB=PC,
在△ABP和△ACP中
$\left\{\begin{array}{l}{AB=AC}\\{∠ABP=∠ACP}\\{BP=CP}\end{array}\right.$,
∴△ABP≌△ACP,
∴∠BAP=∠CAP,
∴AP平分∠BAC;
(2)∵BQ=PB+PA,
而BQ=BP+PQ,
∴PA=PQ,
∴∠PQA=∠PAQ=∠PAC+∠2,
∵AQ∥PC,
∴∠1=∠2,
设∠1=∠3=x,则∠PQA=∠PAQ=30°+x,
∴∠APQ=180°-2(30°+x)=x+30°,解得x=30°,
∴∠PBC=15°,
当MP=MB时,∠BMP=180°-2×15°=150°;
当PM=PB时,∠BMP=15°;
当BM=BP时,∠BMP=$\frac{1}{2}$(180°-15°)=82.5°.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了等腰三角形的性质.

 阅读快车系列答案
阅读快车系列答案| A. | -2 | B. | 4 | C. | 0 | D. | 8 |
 抛物线y=ax2+bx+c的图象如图所示,则当y≤3时,求x的取值范围.
抛物线y=ax2+bx+c的图象如图所示,则当y≤3时,求x的取值范围.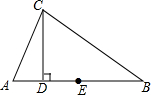 如图,在△ABC中,∠A=2∠B,CD⊥AB,垂足为D,E为AB的中点,若AC=8cm,求DE的长.
如图,在△ABC中,∠A=2∠B,CD⊥AB,垂足为D,E为AB的中点,若AC=8cm,求DE的长.