��Ŀ����
18����ͼ1����֪������C1��y=ax2-2�Ķ���Ϊ��P����x����A��B���㣨A����B����ࣩ����sin��ABP=$\frac{{2\sqrt{13}}}{13}$����1���������ߵĺ�������ʽ��
��2������A��ֱ�߽���һ�����������ڵ�C����y���ڵ�D������ABC�������y���Ϊ1��5�������֣���ֱ��AC�Ľ���ʽ��
��3����ͼ2����������C1�ƶ���P��ת180��õ�������C2��QΪy�Ḻ�����ϵ�һ�㣬����Q����ֱ�߽���ת���������C2��M��N������ͬ�㣬�Ƿ���������ĵ�Q��ʹ�á�MPN��Ϊֱ�ǣ������ڣ������Q������ꣻ�������ڣ���˵�����ɣ�
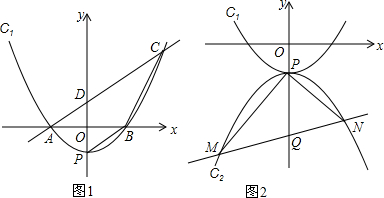
���� ��1��ͨ�������߽���ʽ����P��0��-2����ͨ����ֱ�������κ������ߵĶԳ��������A��B�����꣬������������������������߽���ʽ��
��2����ͼ1����C��CE��x����E���������������Σ���AOD�ס�AEC�����ø����������εĶ�Ӧ�߳ɱ������AE=9����OE=6�����ã�1���е������߽���ʽ�����A��C�����꣬���ô���ϵ��������ֱ��AC�Ľ���ʽΪ��$y=\frac{2}{3}x+2$��
��3�����ڣ���Q��0��b����M��x1��y1��N��x2��y2����ֱ��MN�Ľ���ʽΪ��y=kx+b��k��0����
��ͼ2���ɶ��κ���ͼ��ļ��α任���������C2�Ľ���ʽΪy=-$\frac{2}{9}$x2-2��������C2��ֱ�߷������������飬�ɸ���ϵ���Ĺ�ϵ�õ���x1+x2=-$\frac{9}{2}$k��x1•x2=$\frac{9}{2}$��b+2��
�ֱ��M��N��y��Ĵ��߶�ME��NF������ֱ�ΪE��F���������������Ρ�MPE�ס�PNF���ɸ����������εĶ�Ӧ�߳ɱ�����֪x1x2=$\frac{9}{2}$����b+2=-$\frac{81}{4}$���������b��ֵ�����Ե�Q�����꣨0��-$\frac{13}{2}$����
��� �⣺��1����sin��ABP=$\frac{{2\sqrt{13}}}{13}$��P��0��-2����
��OB=3��
��B��3��0����A��-3��0����
��9a-2=0����� a=$\frac{2}{9}$��
�������ߵĽ���ʽΪy=$\frac{2}{9}$x2-2��
��2����ͼ1����C��CE��x����E��
��S��AOD=$\frac{1}{6}$S��ABC��AB=2OA��
��CE=3OD��
�ߡ�AOD�ס�AEC��
��$\frac{OD}{CE}=\frac{OA}{AE}=\frac{1}{3}$��
��OA=3��
��AE=9��
��OE=6��
��y=$\frac{2}{9}$x2-2����x=6����y=6��
��C��6��6����
��A��-3��0����
��ֱ��AC�Ľ���ʽΪ��$y=\frac{2}{3}x+2$��
��3���𣺴��ڣ���Q��0��b�� M��x1��y1��N��x2��y2�� ֱ��MN�Ľ���ʽΪ��y=kx+b��k��0����
�������֪��������C2�Ľ���ʽΪy=-$\frac{2}{9}$x2-2
��$\left\{\begin{array}{l}y=kx+b\\ y=-\frac{2}{9}{x^2}-2\end{array}\right.$�ã�$\frac{2}{9}$x2+kx+b+2=0��
��x1+x2=-$\frac{9}{2}$k��x1•x2=$\frac{9}{2}$��b+2����
�ֱ��M��N��y��Ĵ��߶�ME��NF������ֱ�ΪE��F
�ߡ�MPN=90�㣬
����֤��MPE�ס�PNF��
��$\frac{ME}{PF}=\frac{PE}{NF}$
�ࣨ-2-y1����-2-y2��=-x1x2��
��-2-y1=$\frac{2}{9}$x12-2-y2=$\frac{2}{9}$x22
��$\frac{4}{81}{x_1}^2{x_2}^2=-{x_1}{x_2}$��
��b��-2��
��x1x2��0��
��x1x2=$\frac{9}{2}$��b+2��=-$\frac{81}{4}$��
��b=-$\frac{13}{2}$��
��Q��0��-$\frac{13}{2}$����
���� ���⿼���˶��κ����ۺ��⣬�����漰���˴���ϵ������һ�κ��������κ�������ʽ�����κ���ͼ���ϵ�����������Ͷ��κ���ͼ��ļ��α任�����������ε��ж������ʵ�֪ʶ�㣮������ѵ��Ǹ����������������ߣ��������������Σ��������������εĶ�Ӧ�߳ɱ�����������߶εij��ȣ��Ӷ������ص�����꣮

 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�| A�� | ������ | B�� | ���� | C�� | ���� | D�� | Բ |
| A�� | 3.18��106 | B�� | 3.19��106 | C�� | 3.1��106 | D�� | 3.2��106 |
| A�� | 45�� | B�� | 60�� | C�� | 75���15�� | D�� | 45���15�� |
| A�� | 5+4$\sqrt{2}$ | B�� | $\sqrt{113}$+7 | C�� | 2$\sqrt{5}$+$\sqrt{41}$ | D�� | ���϶����� |
 ��ͼ����AOC�͡�BOD����ֱ�ǣ������AOB=150�㣬��ô��COD=30�ȣ�
��ͼ����AOC�͡�BOD����ֱ�ǣ������AOB=150�㣬��ô��COD=30�ȣ� ��ͼ��4��4�����е�cosB��ֵ����$\frac{2\sqrt{5}}{5}$��
��ͼ��4��4�����е�cosB��ֵ����$\frac{2\sqrt{5}}{5}$��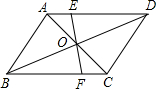 ��ͼ�����ı���ABCD�У�AD��BC���Խ���AC��BD���ڵ�O������O��ֱ��EF��AD�ڵ�E����BC�ڵ�F��OE=OF��
��ͼ�����ı���ABCD�У�AD��BC���Խ���AC��BD���ڵ�O������O��ֱ��EF��AD�ڵ�E����BC�ڵ�F��OE=OF��