题目内容
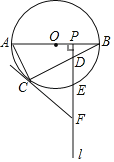
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以AB为直径的半圆O交AC于点D,点E是
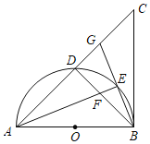
,以AB为直径的半圆O交AC于点D,点E是![]() 上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:![]() ;
;
(2)填空:
①若![]() ,且点E是
,且点E是![]() 的中点,则DF的长为 ;
的中点,则DF的长为 ;
②取![]() 的中点H,当
的中点H,当![]() 的度数为 时,四边形OBEH为菱形.
的度数为 时,四边形OBEH为菱形.
【答案】(1)见解析(2)①![]() ②30°
②30°
【解析】
(1)利用直径所对的圆周角是直角,可得![]() ,再应用同角的余角相等可得
,再应用同角的余角相等可得![]() ,易得
,易得![]() ,
,![]() 得证;
得证;
(2)作![]() ,应用等弧所对的圆周角相等得
,应用等弧所对的圆周角相等得![]() ,再应用角平分线性质可得结论;由菱形的性质可得
,再应用角平分线性质可得结论;由菱形的性质可得![]() ,结合三角函数特殊值可得
,结合三角函数特殊值可得![]() .
.
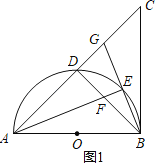
解:(1)证明:如图1,![]() ,
,![]() ,
,
![]()
![]() AB是
AB是![]() 的直径,
的直径,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ;
;
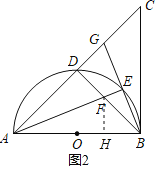
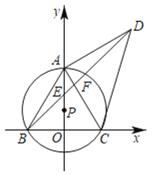
(2)①如图2,过F作![]() 于H,
于H,![]() 点E是
点E是![]() 的中点,
的中点,
![]()
![]() ,
,![]()
![]()
![]() ,
,
![]() ,即
,即![]()
![]() ,
,
![]() ,即
,即![]() ,
,![]()
![]()
故答案为![]() .
.

②连接OE,EH,![]() 点H是
点H是![]() 的中点,
的中点,
![]() ,
,
![]()
![]()
![]()
![]() 四边形OBEH为菱形,
四边形OBEH为菱形,
![]()
![]()
![]() .
.
故答案为:![]()

练习册系列答案
相关题目
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小菲根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小菲的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是___________________.
的取值范围是___________________.
(2)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | … |
| … |
|
|
|
|
|
|
| 2 |
|
| … |
表中![]() 的值为____________________________.
的值为____________________________.
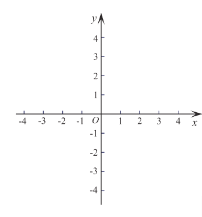
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
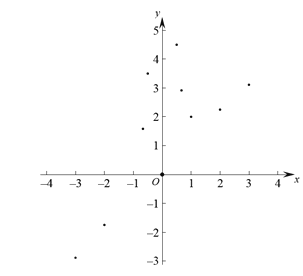
(4)根据画出的函数图象,写出:
①![]() 时,对应的函数值
时,对应的函数值![]() 约为__________________(结果保留一位小数);
约为__________________(结果保留一位小数);
②该函数的一条性质:________________________________________________________.