题目内容
(1)当k为何值时,一次函数y=x-3的图象与二次函数y=x2-8x-(2k+1)的图象有两个交点;(2)试写出k的一个数值,使这两个函数图象的交点的横坐标一个大于1,一个小于1.
分析:(1)解有两个函数解析式组成的方程组,得到关于x的一元二次方程,因为有两个交点,故△>0,即可求.
(2)有x2-9x-2k+2=0,若令-2k+2=0(有很多值),即k=1,x1=0,x2=9,符合题目要求.
(2)有x2-9x-2k+2=0,若令-2k+2=0(有很多值),即k=1,x1=0,x2=9,符合题目要求.
解答:解:(1)令x-3=x2-8x-(2k+1),则x2-9x-2k+2=0(3分)
因为一次函数图象与二次函数图象有两个交点,
所以81-4(-2k+2)>0,
即k>-
(7分)
(2)设x(x-9)=0则x2-9x=0(11分)
令-2k+2=0,得k=1
所以当k=1时,所给的一次函数与二次函数图象的交点的横坐标一个大于1,一个小于1.(15分)
因为一次函数图象与二次函数图象有两个交点,
所以81-4(-2k+2)>0,
即k>-
| 73 |
| 8 |
(2)设x(x-9)=0则x2-9x=0(11分)
令-2k+2=0,得k=1
所以当k=1时,所给的一次函数与二次函数图象的交点的横坐标一个大于1,一个小于1.(15分)
点评:本题利用了解方程组,以及一元二次方程根的判别式等知识.

练习册系列答案
相关题目



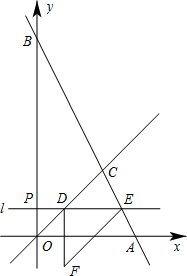 (2012•金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.
(2012•金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°. 某居民小区要在一块一边靠墙(墙长13m)的空地上建一个矩形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),
某居民小区要在一块一边靠墙(墙长13m)的空地上建一个矩形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),