ÌâÄżÄÚÈĘ
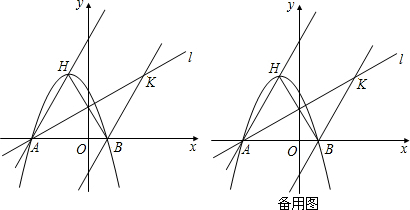
ÒŃÖȘÈçÍŒŁŹ¶țŽÎșŻÊęy=ax2+2ax-3aŁšaĄÙ0Ł©ÍŒÏó”Ķ„”ăÎȘHŁŹÓëxÖ᜻ÓÚAĄąBÁœ”㣚BÔÚA”ăÓÒČàŁ©ŁŹ”ăHĄąBčŰÓÚÖ±ÏßlŁșy=
x+
¶ÔłÆŁź
Łš1Ł©ÇóAĄąBÁœ”ăŚű±êŁŹČąÖ€Ăś”ăAÔÚÖ±ÏßlÉÏŁ»
Łš2Ł©Çó¶țŽÎșŻÊęœâÎöÊœŁ»
Łš3Ł©Éè”ăsÊÇÈęœÇĐÎABHÉÏ”ÄÒ»¶Ż”㣏ŽÓ”ăAŃŰŚĆAHB·œÏòÒÔĂżĂë1žö”„λł€¶ÈÒƶŻŁŹÔ˶ŻÊ±ŒäÎȘtĂ룏”œŽï”ăBÊ±ÍŁÖčÔ˶ŻŁź”±tÎȘșÎ֔ʱŁŹÒÔ”ăsÎȘÔČĐÄ”ÄÔČÓëÁœŚű±êÖᶌÏàÇĐŁź
Łš4Ł©čę”ăBŚśÖ±ÏßBKĄÎAHœ»Ö±ÏßlÓÚK”㣏MĄąN·Ö±đÎȘÖ±ÏßAHșÍÖ±ÏßlÉÏ”ÄÁœžö¶Ż”㣏ÁŹœÓHNĄąNMĄąMKŁŹÇóHN+NM+MKș͔ČîĐĄÖ”Łź

| ||
| 3 |
| 3 |
Łš1Ł©ÇóAĄąBÁœ”ăŚű±êŁŹČąÖ€Ăś”ăAÔÚÖ±ÏßlÉÏŁ»
Łš2Ł©Çó¶țŽÎșŻÊęœâÎöÊœŁ»
Łš3Ł©Éè”ăsÊÇÈęœÇĐÎABHÉÏ”ÄÒ»¶Ż”㣏ŽÓ”ăAŃŰŚĆAHB·œÏòÒÔĂżĂë1žö”„λł€¶ÈÒƶŻŁŹÔ˶ŻÊ±ŒäÎȘtĂ룏”œŽï”ăBÊ±ÍŁÖčÔ˶ŻŁź”±tÎȘșÎ֔ʱŁŹÒÔ”ăsÎȘÔČĐÄ”ÄÔČÓëÁœŚű±êÖᶌÏàÇĐŁź
Łš4Ł©čę”ăBŚśÖ±ÏßBKĄÎAHœ»Ö±ÏßlÓÚK”㣏MĄąN·Ö±đÎȘÖ±ÏßAHșÍÖ±ÏßlÉÏ”ÄÁœžö¶Ż”㣏ÁŹœÓHNĄąNMĄąMKŁŹÇóHN+NM+MKș͔ČîĐĄÖ”Łź

·ÖÎöŁșŁš1Ł©Çółö·œłÌax2+2ax-3a=0ŁšaĄÙ0Ł©ŁŹŒŽżÉ”Ă”œA”ăŚű±êșÍB”ăŚű±êŁ»°ŃA”ÄŚű±êŽúÈëÖ±ÏßlŒŽżÉĆжÏAÊÇ·ńÔÚÖ±ÏßÉÏŁ»
Łš2Ł©žùŸĘ”ăHĄąBčŰÓÚčęA”ă”ÄÖ±ÏßlŁșy=
x+
¶ÔłÆŁŹ”ĂłöAH=AB=4ŁŹč궄”ăHŚśHCĄÍABœ»ABÓÚC”㣏ÇółöACșÍHC”Äł€ŁŹ”Ăłö¶„”ăH”ÄŚű±êŁŹŽúÈë¶țŽÎșŻÊęœâÎöÊœŁŹÇółöaŁŹŒŽżÉ”Ă”œ¶țŽÎșŻÊęœâÎöÊœŁ»
Łš3Ł©ÊŚÏÈĆжšĄśABHÊǔȱßÈęœÇĐÎŁŹœű¶űččÔìÖ±œÇÈęœÇĐΔóöt”ÄÖ”ŒŽżÉŁ»
Łš4Ł©”ĂłöÖ±ÏßAHŁŹBK”ÄœâÎöÊœŁŹ”Ă”œ·œłÌŚé
ŁŹŒŽżÉÇółöK”ÄŚű±êŁŹžùŸĘ”ăHĄąBčŰÓÚÖ±ÏßAK¶ÔłÆŁŹ”ĂłöHN+MN”ÄŚîĐĄÖ”ÊÇMBŁŹčę”ăKŚśÖ±ÏßAH”Ä¶ÔłÆ”ăQŁŹÁŹœÓQKŁŹœ»Ö±ÏßAHÓÚEŁŹ”Ă”œBM+MK”ÄŚîĐĄÖ”ÊÇBQŁŹŒŽBQ”Äł€ÊÇHN+NM+MK”ÄŚîĐĄÖ”ŁŹÓÉčŽčɶšÀí”ĂQB=8ŁŹŒŽżÉ”ĂłöŽđ°žŁź
Łš2Ł©žùŸĘ”ăHĄąBčŰÓÚčęA”ă”ÄÖ±ÏßlŁșy=
| ||
| 3 |
| 3 |
Łš3Ł©ÊŚÏÈĆжšĄśABHÊǔȱßÈęœÇĐÎŁŹœű¶űččÔìÖ±œÇÈęœÇĐΔóöt”ÄÖ”ŒŽżÉŁ»
Łš4Ł©”ĂłöÖ±ÏßAHŁŹBK”ÄœâÎöÊœŁŹ”Ă”œ·œłÌŚé
|
œâŽđŁșœâŁșŁš1Ł©ÒÀÌâÒ⣏”Ăax2+2ax-3a=0ŁšaĄÙ0Ł©ŁŹ
ŒŽx2+2x-3=0ŁŹ
œâ”Ăx1=-3ŁŹx2=1ŁŹ
ĄßB”ăÔÚA”ăÓÒČàŁŹ
ĄàA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹB”ăŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ
ŽđŁșAĄąBÁœ”ăŚű±ê·Ö±đÊÇŁš-3ŁŹ0Ł©ŁŹŁš1ŁŹ0Ł©Łź
ĄßÖ±ÏßlŁșy=
x+
ŁŹ
”±x=-3ʱŁŹy=
ĄÁŁš-3Ł©+
=0ŁŹ
Ąà”ăAÔÚÖ±ÏßlÉÏŁź
Łš2Ł©Ąß”ăHĄąBčŰÓÚčęA”ă”ÄÖ±ÏßlŁșy=
x+
¶ÔłÆŁŹ
ĄàAH=AB=4ŁŹ
ÈçÍŒ1ŁŹč궄”ăHŚśHCĄÍABœ»ABÓÚC”㣏
ÔòAC=
AB=2ŁŹHC=2
ŁŹ
Ąà¶„”ăHŁš-1ŁŹ2
Ł©ŁŹ
ŽúÈë¶țŽÎșŻÊęœâÎöÊœŁŹœâ”Ăa=-
ŁŹ
Ąà¶țŽÎșŻÊęœâÎöÊœÎȘy=-
x2-
x+
ŁŹ
ŽđŁș¶țŽÎșŻÊęœâÎöÊœÎȘy=-
x2-
x+
ŁŹ
Łš3Ł©ĄßA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹ”ăHŁš-1ŁŹ2
Ł©ŁŹ
ĄàAH=
=4ŁŹ
ĄßB”ăŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ”ăHŁš-1ŁŹ2
Ł©ŁŹ
ĄàBH=
=4ŁŹ
ĄßA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹB”ăŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ
ĄàAB=4ŁŹŒŽAB=AH=BH=4ŁŹ
ĄàĄśABHÊǔȱßÈęœÇĐÎŁŹ
ÈçÍŒ2ŁŹčę”ăSŚśSCĄÍABÓÚ”ăCŁŹčę”ăS1ŚśS1EĄÍABÓÚ”ăEŁŹ
Éè”±tĂëʱŁŹÒÔ”ăsÎȘÔČĐÄ”ÄÔČÓëÁœŚű±êÖᶌÏàÇĐŁź
ÔòAS=tŁŹAC=
tŁŹSC=
tŁŹ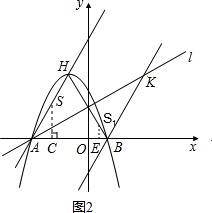
ŽËʱSC=COŁŹ
ŒŽ
t=3-
tŁŹ
œâ”ĂŁșt=3Łš
-1Ł©ŁŹ
ÍŹÀíżÉ”ĂŁșS1B=AH+HB-t=8-tŁŹBE=
ŁŹS1E=
ŁŹ
”±EO=S1EŁŹ
ŒŽ1-
=
ŁŹ
œâ”ĂŁșt=9-
ŁŹ
čÊ”±t=3Łš
-1Ł©»òt=9-
ʱŁŹÒÔ”ăsÎȘÔČĐÄ”ÄÔČÓëÁœŚű±êÖᶌÏàÇĐŁź
Łš4Ł©ĄßA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹ”ăHŁš-1ŁŹ2
Ł©ŁŹ
Ąàœ«Áœ”ăŽúÈëœâÎöÊœy=kx+bŁŹ
”Ăłö
ŁŹ
œâ”ĂŁș
ŁŹ
čÊÖ±ÏßAH”ÄœâÎöÊœÎȘy=
x+3
ŁŹ
ĄßÖ±ÏßBKĄÎAHœ»Ö±ÏßlÓÚK”㣏
ĄàÖ±ÏßBK”ÄœâÎöÊœÎȘŁșy=
x+bŁŹ
œ«B”ăŚű±êŽúÈëÇółöŁŹ
Ö±ÏßBK”ÄœâÎöÊœÎȘŁșy=
x-
ŁŹ
ÓÉ
ŁŹ
œâ”Ă
ŁŹ
ŒŽKŁš3ŁŹ2
Ł©ŁŹ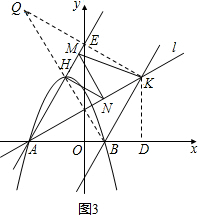
ÔòBK=4ŁŹ
Ąß”ăHĄąBčŰÓÚÖ±ÏßAK¶ÔłÆŁŹKŁš3ŁŹ2
Ł©ŁŹ
ĄàHN+MN”ÄŚîĐĄÖ”ÊÇMBŁŹKD=KE=2
ŁŹ
ÈçÍŒ3ŁŹčę”ăKŚśÖ±ÏßAH”Ä¶ÔłÆ”ăQŁŹÁŹœÓQKŁŹœ»Ö±ÏßAHÓÚEŁŹKD=KE=2
ŁŹ
ÔòQM=MKŁŹQE=EK=2
ŁŹAEĄÍQKŁŹ
ĄàBM+MK”ÄŚîĐĄÖ”ÊÇBQŁŹŒŽBQ”Äł€ÊÇHN+NM+MK”ÄŚîĐĄÖ”ŁŹ
ĄßBKĄÎAHŁŹ
ĄàĄÏBKQ=ĄÏHEQ=90ĄăŁŹ
ÓÉčŽčɶšÀí”ĂQB=8ŁŹ
ĄàHN+NM+MK”ÄŚîĐĄÖ”ÎȘ8ŁŹ
ŽđŁșHN+NM+MKș͔ČîĐĄÖ”ÊÇ8Łź
ŒŽx2+2x-3=0ŁŹ
œâ”Ăx1=-3ŁŹx2=1ŁŹ
ĄßB”ăÔÚA”ăÓÒČàŁŹ
ĄàA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹB”ăŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ
ŽđŁșAĄąBÁœ”ăŚű±ê·Ö±đÊÇŁš-3ŁŹ0Ł©ŁŹŁš1ŁŹ0Ł©Łź
ĄßÖ±ÏßlŁșy=
| ||
| 3 |
| 3 |
”±x=-3ʱŁŹy=
| ||
| 3 |
| 3 |

Ąà”ăAÔÚÖ±ÏßlÉÏŁź
Łš2Ł©Ąß”ăHĄąBčŰÓÚčęA”ă”ÄÖ±ÏßlŁșy=
| ||
| 3 |
| 3 |
ĄàAH=AB=4ŁŹ
ÈçÍŒ1ŁŹč궄”ăHŚśHCĄÍABœ»ABÓÚC”㣏
ÔòAC=
| 1 |
| 2 |
| 3 |
Ąà¶„”ăHŁš-1ŁŹ2
| 3 |
ŽúÈë¶țŽÎșŻÊęœâÎöÊœŁŹœâ”Ăa=-
| ||
| 2 |
Ąà¶țŽÎșŻÊęœâÎöÊœÎȘy=-
| ||
| 2 |
| 3 |
3
| ||
| 2 |
ŽđŁș¶țŽÎșŻÊęœâÎöÊœÎȘy=-
| ||
| 2 |
| 3 |
3
| ||
| 2 |
Łš3Ł©ĄßA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹ”ăHŁš-1ŁŹ2
| 3 |
ĄàAH=
22+(2
|
ĄßB”ăŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ”ăHŁš-1ŁŹ2
| 3 |
ĄàBH=
22+(2
|
ĄßA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹB”ăŚű±êÎȘŁš1ŁŹ0Ł©ŁŹ
ĄàAB=4ŁŹŒŽAB=AH=BH=4ŁŹ
ĄàĄśABHÊǔȱßÈęœÇĐÎŁŹ
ÈçÍŒ2ŁŹčę”ăSŚśSCĄÍABÓÚ”ăCŁŹčę”ăS1ŚśS1EĄÍABÓÚ”ăEŁŹ
Éè”±tĂëʱŁŹÒÔ”ăsÎȘÔČĐÄ”ÄÔČÓëÁœŚű±êÖᶌÏàÇĐŁź
ÔòAS=tŁŹAC=
| 1 |
| 2 |
| ||
| 2 |

ŽËʱSC=COŁŹ
ŒŽ
| ||
| 2 |
| 1 |
| 2 |
œâ”ĂŁșt=3Łš
| 3 |
ÍŹÀíżÉ”ĂŁșS1B=AH+HB-t=8-tŁŹBE=
| 8-t |
| 2 |
| ||
| 2 |
”±EO=S1EŁŹ
ŒŽ1-
| 8-t |
| 2 |
| ||
| 2 |
œâ”ĂŁșt=9-
| 3 |
čÊ”±t=3Łš
| 3 |
| 3 |
Łš4Ł©ĄßA”ăŚű±êÎȘŁš-3ŁŹ0Ł©ŁŹ”ăHŁš-1ŁŹ2
| 3 |
Ąàœ«Áœ”ăŽúÈëœâÎöÊœy=kx+bŁŹ
”Ăłö
|
œâ”ĂŁș
|
čÊÖ±ÏßAH”ÄœâÎöÊœÎȘy=
| 3 |
| 3 |
ĄßÖ±ÏßBKĄÎAHœ»Ö±ÏßlÓÚK”㣏
ĄàÖ±ÏßBK”ÄœâÎöÊœÎȘŁșy=
| 3 |
œ«B”ăŚű±êŽúÈëÇółöŁŹ
Ö±ÏßBK”ÄœâÎöÊœÎȘŁșy=
| 3 |
| 3 |
ÓÉ
|
œâ”Ă
|
ŒŽKŁš3ŁŹ2
| 3 |

ÔòBK=4ŁŹ
Ąß”ăHĄąBčŰÓÚÖ±ÏßAK¶ÔłÆŁŹKŁš3ŁŹ2
| 3 |
ĄàHN+MN”ÄŚîĐĄÖ”ÊÇMBŁŹKD=KE=2
| 3 |
ÈçÍŒ3ŁŹčę”ăKŚśÖ±ÏßAH”Ä¶ÔłÆ”ăQŁŹÁŹœÓQKŁŹœ»Ö±ÏßAHÓÚEŁŹKD=KE=2
| 3 |
ÔòQM=MKŁŹQE=EK=2
| 3 |
ĄàBM+MK”ÄŚîĐĄÖ”ÊÇBQŁŹŒŽBQ”Äł€ÊÇHN+NM+MK”ÄŚîĐĄÖ”ŁŹ
ĄßBKĄÎAHŁŹ
ĄàĄÏBKQ=ĄÏHEQ=90ĄăŁŹ
ÓÉčŽčɶšÀí”ĂQB=8ŁŹ
ĄàHN+NM+MK”ÄŚîĐĄÖ”ÎȘ8ŁŹ
ŽđŁșHN+NM+MKș͔ČîĐĄÖ”ÊÇ8Łź
”ăÆÀŁș±ŸÌâÖśÒȘżŒČéÁ˶ÔčŽčɶšÀíŁŹœâ¶țÔȘÒ»ŽÎ·œłÌŚéŁŹ¶țŽÎșŻÊęÓëÒ»ÔȘ¶țŽÎ·œłÌŁŹ¶țŽÎșŻÊęÓëXÖá”Äœ»”㣏ÓĂŽę¶šÏ”Êę·šÇó¶țŽÎșŻÊę”ÄœâÎöÊœ”ÈÖȘʶ”ă”ÄÀíœâșÍŐÆÎŐŁŹŚÛșÏÔËÓĂŐâĐ©ĐÔÖÊœűĐĐŒÆËăÊÇœâŽËÌâ”ÄčŰŒüŁŹŽËÌâÊÇÒ»žöŚÛșÏĐԱȜÏÇż”ÄÌâÄżŁŹÓĐÒ»¶š”ÄÄŃ¶ÈŁź

Á·Ï°ČáÏ”ÁĐŽđ°ž
ÏàčŰÌâÄż
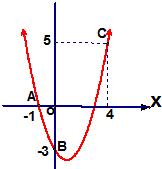 16ĄąÒŃÖȘÈçÍŒŁŹ¶țŽÎșŻÊęy=ax2+bx+c”ÄÍŒÏóčęAĄąBĄąCÈę”ă
16ĄąÒŃÖȘÈçÍŒŁŹ¶țŽÎșŻÊęy=ax2+bx+c”ÄÍŒÏóčęAĄąBĄąCÈę”ă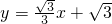 ¶ÔłÆŁź
¶ÔłÆŁź