题目内容
某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为扩大销售增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价一元，市场每天可多售2件，问他降价多少元时，才能使每天所赚的利润最大？并求出最大利润．
考点：由实际问题抽象出一元二次方程
专题：
分析：设每件衬衫应降价x元，利润为w元，由于每件衬衫每降价1元，商场平均每天可多售出2件，所以降价x元后每天可以售出：（20+2x）件，此时每件盈利：（40-x）元，每天盈利w=（20+2x）（40-x），求出极值即可得出答案．
解答：解：设每件衬衫应降价x元，利润为w元，
根据题意，商场降价后每天盈利=每件的利润×卖出的件数，
则有w=（20+2x）（40-x）
=-2x2+60x+800
=-2（x-15）2+1250
即当x=15时，w有最大值，为1250，
答：每件衬衫应降价15元，可获得最大利润，最大利润为1250．
根据题意，商场降价后每天盈利=每件的利润×卖出的件数，
则有w=（20+2x）（40-x）
=-2x2+60x+800
=-2（x-15）2+1250
即当x=15时，w有最大值，为1250，
答：每件衬衫应降价15元，可获得最大利润，最大利润为1250．
点评：此题主要考查了由实际问题抽象出一元二次方程，根据降价后销量的变化得出等式方程是解题关键．
练习册系列答案
相关题目
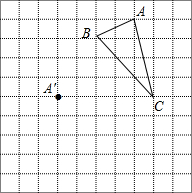在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC三个顶点的位置如图所示，现将△ABC平移，使点A移动到点A′，点B′、C′分别是B、C的对应点．
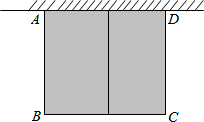如图，有长为24米的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体（墙体的最大可用长度a=10米）．如果AB的长为x，面积为y，
下列事件是必然事件的是（ ）
| A、阴天一定会下雨 |
| B、在装有5个红球的袋中摸出1个球，是红球 |
| C、打开电视机，正在播放动画片 |
| D、某彩票中奖率是1%，买100张一定会中奖 |