题目内容
1. 一次函数y=-x+1(0≤x≤10)与反比例函数y=$\frac{1}{x}$(-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1,y1),(x2,y2)是图象上两个不同的点,若y1=y2,则x1+x2的取值范围是( )
一次函数y=-x+1(0≤x≤10)与反比例函数y=$\frac{1}{x}$(-10≤x<0)在同一平面直角坐标系中的图象如图所示,点(x1,y1),(x2,y2)是图象上两个不同的点,若y1=y2,则x1+x2的取值范围是( )| A. | -$\frac{89}{10}$≤x≤1 | B. | -$\frac{89}{10}$≤x≤$\frac{89}{9}$ | C. | -$\frac{89}{9}$≤x≤$\frac{89}{10}$ | D. | 1≤x≤$\frac{89}{10}$ |
分析 由x的取值范围结合y1=y2可求出y的取值范围,根据y关于x的关系式可得出x关于y的关系式,利用做差法求出x=1-y+$\frac{1}{y}$再-9≤y≤-$\frac{1}{10}$中的单调性,依此单调性即可求出x1+x2的取值范围.
解答 解:当x=-10时,y=$\frac{1}{x}$=-$\frac{1}{10}$;
当x=10时,y=-x+1=-9,
∴-9≤y1=y2≤-$\frac{1}{10}$.
设x1<x2,则y2=-x2+1、y1=$\frac{1}{{x}_{1}}$,
∴x2=1-y2,x1=$\frac{1}{{y}_{1}}$,
∴x1+x2=1-y2+$\frac{1}{{y}_{1}}$.
设x=1-y+$\frac{1}{y}$(-9≤y≤-$\frac{1}{10}$),-9≤ym<yn≤-$\frac{1}{10}$,
则xn-xm=ym-yn+$\frac{1}{{y}_{n}}$-$\frac{1}{{y}_{m}}$=(ym-yn)(1+$\frac{1}{{y}_{m}{y}_{n}}$)<0,
∴x=1-y+$\frac{1}{y}$中x值随y值的增大而减小,
∴1-(-$\frac{1}{10}$)-10=-$\frac{89}{10}$≤x≤1-(-9)-$\frac{1}{9}$=$\frac{89}{9}$.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征以及一次函数图象上点的坐标特征,找出x=1-y+$\frac{1}{y}$在-9≤y≤-$\frac{1}{10}$中的单调性是解题的关键.

练习册系列答案
相关题目
 如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=-2x+m+6经过点B,交y轴于点E(0,6).
如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=-2x+m+6经过点B,交y轴于点E(0,6).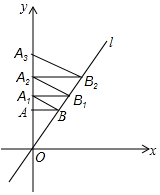 如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,按此作法继续下去,则点A2017的纵坐标为$(\frac{4}{3})^{2017}$.
如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,按此作法继续下去,则点A2017的纵坐标为$(\frac{4}{3})^{2017}$. 如图,将△ABC沿DE折叠,使得点B与点A重合,△ADC的周长为17cm,AE=5cm,则△ABC的周长为27cm.
如图,将△ABC沿DE折叠,使得点B与点A重合,△ADC的周长为17cm,AE=5cm,则△ABC的周长为27cm.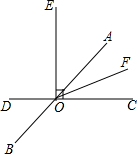 如图所示,直线AB,CD相交于点O,OF平分∠AOC,EO⊥CD于点O,且∠DOF=160°,求∠BOE的度数.
如图所示,直线AB,CD相交于点O,OF平分∠AOC,EO⊥CD于点O,且∠DOF=160°,求∠BOE的度数.