题目内容
4．解方程：（1）$\frac{6}{x-3}$-$\frac{2x-3}{4（x-3）}$=1
（2）$\frac{1}{x+3}$-$\frac{2}{3-x}$=$\frac{9}{{x}^{2}-9}$．
分析 两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：（1）去分母得：24-2x+3=4x-12，
解得：x=6.5，
经检验x=6.5是分式方程的解；
（2）去分母得：x-3+2x+6=9，
解得：x=2，
经检验x=2是分式方程的解．
点评 此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
练习册系列答案
相关题目
1．
一次函数y=-x+1（0≤x≤10）与反比例函数y=$\frac{1}{x}$（-10≤x＜0）在同一平面直角坐标系中的图象如图所示，点（x1，y1），（x2，y2）是图象上两个不同的点，若y1=y2，则x1+x2的取值范围是（ ）
一次函数y=-x+1（0≤x≤10）与反比例函数y=$\frac{1}{x}$（-10≤x＜0）在同一平面直角坐标系中的图象如图所示，点（x1，y1），（x2，y2）是图象上两个不同的点，若y1=y2，则x1+x2的取值范围是（ ）| A． | -$\frac{89}{10}$≤x≤1 | B． | -$\frac{89}{10}$≤x≤$\frac{89}{9}$ | C． | -$\frac{89}{9}$≤x≤$\frac{89}{10}$ | D． | 1≤x≤$\frac{89}{10}$ |
已知，如图，平行四边形ABCD中，AC、BD相交于点O，点E在AD上，点F在CB上，且AE=CF，求证：OE=OF．
16．
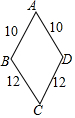如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框，为保证稳定要在BD间加一根木条．设该木条的长为xcm，则x的取值范围是（ ）
如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框，为保证稳定要在BD间加一根木条．设该木条的长为xcm，则x的取值范围是（ ）| A． | 0＜x＜20 | B． | 2＜x＜20 | C． | 0＜x＜24 | D． | 2＜x＜24 |
