题目内容
18. 如图,AB∥CD,∠CDE=121°,GF交∠DEB的平分线EF于点F,∠AGF=140°,求∠F的度数.
如图,AB∥CD,∠CDE=121°,GF交∠DEB的平分线EF于点F,∠AGF=140°,求∠F的度数.
分析 先根据平行线的性质求出∠AED与∠DEB的度数,再由角平分线的性质求出∠DEF的度数,进而可得出∠GEF的度数,再根据三角形外角的性质即可得出结论.
解答 解:∵AB∥CD,∠CDE=121°,
∴∠AED=180°-121°=59°,∠DEB=121°.
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=$\frac{1}{2}$×121°=60.5°,
∴∠GEF=59°+60.5°=119.5°.
∵∠AGF=140°,
∴∠F=∠AGF-∠GEF=140°-119.5°=20.5°.
点评 本题考查的是平行线的性质、角平分线的定义、三角形的外角性质;熟记两直线平行,同旁内角互补,内错角相等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列计算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | a8÷a4=a2 | C. | (a-b)2=a2-b2 | D. | 3m+4n=7mn |
3.已知三角形的两边长分别为8和4,则第三边长可能是( )
| A. | 3 | B. | 4 | C. | 8 | D. | 12 |
8.已知反比例函数的 图象经过点P(2,-1),则这个反比例函数的解析式为( )
| A. | y=$\frac{1}{x}$ | B. | y=-$\frac{1}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{2}{x}$ |
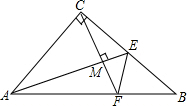 如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
如图,△ABC中,AC=BC,∠ACB=90°.若AE为△ABC的中线,CF⊥AE,垂足为M,交AB于F点,求证:
 如图,在△ABC中,D是BC上一点,AC=CD,∠DAB=10°,则∠CAB-∠B=20°.
如图,在△ABC中,D是BC上一点,AC=CD,∠DAB=10°,则∠CAB-∠B=20°.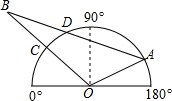 如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.
如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.