题目内容
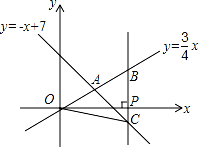
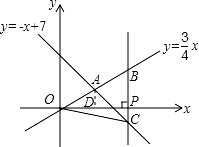
如图,在平面直角坐标系 xOy 中,已知正比例函数 y=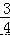 x 与一次函数 y=﹣x+7 的图象交于点 A.
x 与一次函数 y=﹣x+7 的图象交于点 A.
(1)求点 A 的坐标;
设 x 轴上有一点 P(a,0),过点 P 作 x 轴的垂线(垂线位于点 A 的右侧),分别交 y=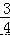 x 和 y=﹣x+7
x 和 y=﹣x+7
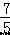 的图象于点 B、C,连接 OC.若 BC= OA,求△OBC 的面积.
的图象于点 B、C,连接 OC.若 BC= OA,求△OBC 的面积.
【考点】两条直线相交或平行问题;勾股定理.
【分析】(1)联立两一次函数的解析式求出 x、y 的值即可得出 A 点坐标;
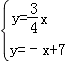 过点 A 作 x 轴的垂线,垂足为 D,在 Rt△OAD 中根据勾股定理求出 OA 的长,故可得出 BC 的长, 根据 P(a,0)可用 a 表示出 B、C 的坐标,故可得出 a 的值,由三角形的面积公式即可得出结论.
过点 A 作 x 轴的垂线,垂足为 D,在 Rt△OAD 中根据勾股定理求出 OA 的长,故可得出 BC 的长, 根据 P(a,0)可用 a 表示出 B、C 的坐标,故可得出 a 的值,由三角形的面积公式即可得出结论.
【解答】解:(1)∵由题意得, ,解得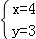 ,
,
∴A(4,3);
过点 A 作 x 轴的垂线,垂足为 D,在 Rt△OAD 中,由勾股定理得,
OA= 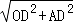 =
= 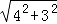 =5.
=5.
∴BC= 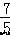 OA=
OA= 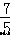 ×5=7.
×5=7.
∵P(a,0),
∴B(a,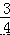 a),C(a,﹣a+7),
a),C(a,﹣a+7),
∴BC= 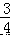 a﹣(﹣a+7)=
a﹣(﹣a+7)= 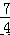 a﹣7,
a﹣7,
∴ 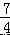 a﹣7=7,解得 a=8,
a﹣7=7,解得 a=8,
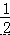
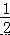 ∴S△OBC= BC•OP= ×7×8=28.
∴S△OBC= BC•OP= ×7×8=28.
【点评】本题考查的是两条直线相交或平行问题,根据题意作出辅助线.构造出直角三角形是解答 此题的关键.

练习册系列答案
相关题目
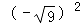 的平方根是 x,64 的立方根是 y,则 x+y 的值为
的平方根是 x,64 的立方根是 y,则 x+y 的值为