题目内容
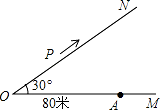
如图,有两条公路 OM、ON 相交成 30°角,沿公路 OM 方向离 O 点 80 米处有一所学校 A.当 重型运输卡车 P 沿道路 ON 方向行驶时,在以 P 为圆心 50 米长为半径的圆形区域内都会受到卡车噪 声的影响,且卡车 P 与学校 A 的距离越近噪声影响越大.若已知重型运输卡车 P 沿道路 ON 方向行 驶的速度为 18 千米/时.
(1)求对学校 A 的噪声影响最大时卡车 P 与学校 A 的距离; 求卡车 P 沿道路 ON 方向行驶一次给学校 A 带来噪声影响的时间.
【考点】勾股定理的应用;垂径定理的应用.
【分析】(1)直接利用直角三角形中 30°所对的边等于斜边的一半求出即可;
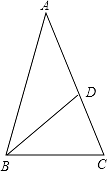
根据题意可知,图中 AB=50m,AD⊥BC,且 BD=CD,∠AOD=30°,OA=80m;再利用垂径定理及 勾股定理解答即可.
【解答】解:(1)过点 A 作 AD⊥ON 于点 D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校 A 的噪声影响最大时卡车 P 与学校 A 的距离为 40 米;
由图可知:以 50m 为半径画圆,分别交 ON 于 B,C 两点,AD⊥BC,BD=CD= BC,OA=80m,
BC,OA=80m,
∵在 Rt△AOD 中,∠AOB=30°,
∴AD=  OA=
OA= 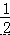 ×80=40m,
×80=40m,
在 Rt△ABD 中,AB=50,AD=40,由勾股定理得:BD= =
=  =30m, 故 BC=2×30=60 米,即重型运输卡车在经过 BC 时对学校产生影响.
=30m, 故 BC=2×30=60 米,即重型运输卡车在经过 BC 时对学校产生影响.
∵重型运输卡车的速度为 18 千米/小时,即 =300 米/分钟,
=300 米/分钟,
∴重型运输卡车经过 BC 时需要 60÷300=0.2(分钟)=12(秒).
答:卡车 P 沿道路 ON 方向行驶一次给学校 A 带来噪声影响的时间为 12 秒.

【点评】此题考查的是垂径定理与勾股定理在实际生活中的运用,解答此题的关键是卡车在哪段路 上


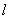 ∥x轴,且直线
∥x轴,且直线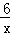 (x>0)和y=﹣
(x>0)和y=﹣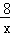 (x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .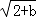 =0,则 a+b 的值是( )
=0,则 a+b 的值是( )
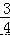 x 与一次函数 y=﹣x+7 的图象交于点 A.
x 与一次函数 y=﹣x+7 的图象交于点 A.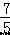 的图象于点 B、C,连接 OC.若 BC= OA,求△OBC 的面积.
的图象于点 B、C,连接 OC.若 BC= OA,求△OBC 的面积.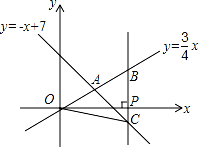
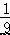 B.﹣
B.﹣ 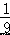 C.9 D.﹣9
C.9 D.﹣9