题目内容
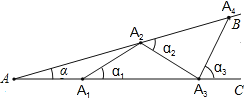
【题目】如图所示，设∠BAC=α（0°
α90°），现把等长的小棒依次向右摆放在两射线之间，并使小棒两端分别落在射线AB，AC上，从点A1开始，其中A1A2为第一根小棒，且A1A2=AA1．
（1）若已经摆放了3根小棒，则∠α1= ；∠α2= ；（用含α的式子表示），若A4A3C=92°，求∠BAC的度数．
（2）若只能摆放6根小棒，求α的范围．
【答案】（1）2α，3α，23°；（2）
【解析】
（1）根据三角形外角的性质和等腰三角形的性质，即可推出∠A4A3C=∠BAC，从而求解；
（2）本题需先根据已知条件，列出不等式，解出α的取值范围，即可得出正确答案．
解：（1）根据三角形外角的性质和等腰三角形的性质可得α1=2α，
则α2=∠A+∠A2A3A=α+α1=3α，α3=4α，
因为∠A4A3C=92°，
则∠BAC=92°÷4=23°；
（2）由题意得：
，
解得 
．
练习册系列答案
相关题目
