题目内容
8.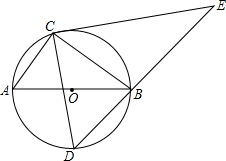 如图,已知AB是⊙O的直径,点C在⊙O上,D是$\widehat{AB}$的中点,过点C作CD的垂线,与DB的延长线相交于点E,若AC=3,BC=4,则DE=$\frac{35\sqrt{2}}{6}$.
如图,已知AB是⊙O的直径,点C在⊙O上,D是$\widehat{AB}$的中点,过点C作CD的垂线,与DB的延长线相交于点E,若AC=3,BC=4,则DE=$\frac{35\sqrt{2}}{6}$.
分析 设CD,AB相交于G,过G作GF⊥BC于F,由D是$\widehat{AB}$的中点,得到∠ACD=∠BCD,由于AB是⊙O的直径,得到∠ACB=90°,求出∠BCD=45°,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,通过△BFG∽△ABC,得到$\frac{GF}{AC}=\frac{BF}{BC}$=$\frac{BG}{AB}$,求出GF=$\frac{12}{7}$,BG=$\frac{20}{7}$,CG=$\frac{12\sqrt{2}}{7}$,AG=$\frac{15}{7}$,由于△ACG∽△DBG,得到$\frac{AC}{BD}=\frac{AG}{DG}$,连接AD,则△ABD是等腰直角三角形,求得DG=$\frac{25\sqrt{2}}{14}$,得到CD=$\frac{7\sqrt{2}}{2}$,通过△ACB∽△CDE,得到$\frac{AC}{CD}=\frac{AB}{DE}$,代入数据即可得到结论.
解答 解:设CD,AB相交于G,过G作GF⊥BC于F,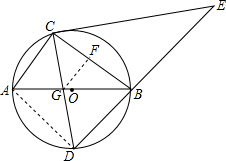 ∵D是$\widehat{AB}$的中点,
∵D是$\widehat{AB}$的中点,
∴∠ACD=∠BCD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCD=45°,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∴CF=GF,
∴FG∥AC,
∴△BFG∽△ABC,
∴$\frac{GF}{AC}=\frac{BF}{BC}$=$\frac{BG}{AB}$,
即$\frac{GF}{3}=\frac{4-GF}{4}$=$\frac{BG}{5}$,
∴GF=$\frac{12}{7}$,BG=$\frac{20}{7}$,
∴CG=$\frac{12\sqrt{2}}{7}$,AG=$\frac{15}{7}$
∵∠A=∠D,∠ACG=∠ABD,
∴△ACG∽△DBG,
∴$\frac{AC}{BD}=\frac{AG}{DG}$,
连接AD,则△ABD是等腰直角三角形,
∴BD=$\frac{5\sqrt{2}}{2}$,
∴DG=$\frac{25\sqrt{2}}{14}$,
∴CD=$\frac{7\sqrt{2}}{2}$,
∵CD⊥DE,
∴∠ACB=∠DCE=90°,∠CAB=∠CDE,
∴△ACB∽△CDE,
∴$\frac{AC}{CD}=\frac{AB}{DE}$,
即$\frac{3}{\frac{7\sqrt{2}}{2}}$=$\frac{5}{DE}$,
∴DE=$\frac{35\sqrt{2}}{6}$.
故答案为:$\frac{35\sqrt{2}}{6}$.
点评 本题考查了相似三角形的判定和性质,圆周角定理,解直角三角形,勾股定理的应用,熟练掌握相似三角形的判定和性质是解题的关键.

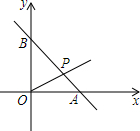 如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、B两点,且A的坐标为(4,0).
如图所示的直角坐标系中,O为坐标原点,直线y=-x+m与x轴、y轴交于A、B两点,且A的坐标为(4,0).



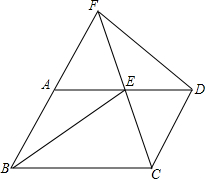 已知平行四边形ABCD,点E为线段AD上一点.联结CE并延长交BA的延长线于点F.联结BE、DF.
已知平行四边形ABCD,点E为线段AD上一点.联结CE并延长交BA的延长线于点F.联结BE、DF.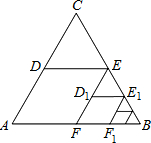 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.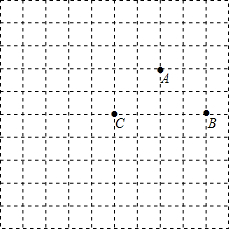 如图,网格中的每一个方格的边长都相等,点A,B,C都在网格的格点上,按要求完成下列各小题.
如图,网格中的每一个方格的边长都相等,点A,B,C都在网格的格点上,按要求完成下列各小题.