题目内容
3.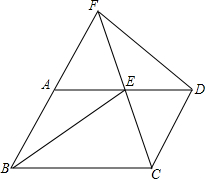 已知平行四边形ABCD,点E为线段AD上一点.联结CE并延长交BA的延长线于点F.联结BE、DF.
已知平行四边形ABCD,点E为线段AD上一点.联结CE并延长交BA的延长线于点F.联结BE、DF.(1)当E为AD的中点时,求证:△DEF与△ABE的面积相等;
(2)当∠ABE=∠DFE时,求证:EF2=AF•DC.
分析 (1)根据平行四边形的性质得到AB∥CD,AB=CD,由平行线的性质得到∠AFC=∠DCF,推出△AFE≌△CDE,根据全等三角形的判定和性质得到AF=CD,根据等底同高的三角形的面积相等即可得到结论;
(2)根据平行线分相等成比例定理得到$\frac{AF}{FE}=\frac{BF}{CF}$,通过△FBE∽△CFD,得到$\frac{EF}{CD}=\frac{BF}{CF}$,等量代换得到$\frac{AF}{EF}=\frac{EF}{CD}$,于是得到结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠AFC=∠DCF,
在△AEF与△CDE中,
$\left\{\begin{array}{l}{∠AFC=∠DCF}\\{∠AEF=∠DEC}\\{AE=DE}\end{array}\right.$,
∴△AFE≌△CDE,
∴AF=CD,
∴AB=AF,
∴S△ABE=S△AEF,
∵AE=EF,
∴S△AEF=S△DEF,
∴△DEF与△ABE的面积相等;
(2)∵AE∥BC,
∴$\frac{AF}{FE}=\frac{BF}{CF}$,
∵∠ABE=∠DFE,∠AFC=∠FCD,
∴△FBE∽△CFD,
∴$\frac{EF}{CD}=\frac{BF}{CF}$,
∴$\frac{AF}{EF}=\frac{EF}{CD}$,
∴EF2=AF•DC.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,全等三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.下列y关于x的函数中,是正比例函数的为( )
| A. | y=x2 | B. | y=$\frac{1}{x}$ | C. | y=x | D. | y=x+1 |
18.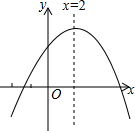 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=2.下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=2.下列结论中正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=2.下列结论中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=2.下列结论中正确的是( )| A. | abc>0 | B. | 5a+c>0 | C. | 4a-b=0 | D. | 9a+3b+c<0 |
15.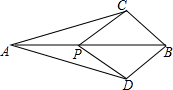 如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( )
如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( )
 如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( )
如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( )| A. | BC=BD | B. | ∠ACB=∠ADB | C. | AC=AD | D. | ∠CAB=∠DAB |
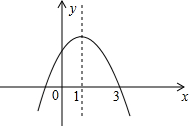 如图,是二次函数y=ax2+bc+c的图象,下列结论中:①a>0②2a+b=0③b2-4av>0④a+b+c<0⑤9a+3b+c=0,其中正确的个数是( )
如图,是二次函数y=ax2+bc+c的图象,下列结论中:①a>0②2a+b=0③b2-4av>0④a+b+c<0⑤9a+3b+c=0,其中正确的个数是( )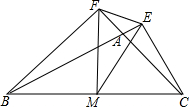 如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.
如图,在△ABC中,CE⊥BA的延长线于E,BF⊥CA的延长线于F,M为BC的中点,分别连接ME、MF、EF.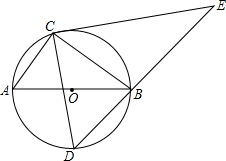 如图,已知AB是⊙O的直径,点C在⊙O上,D是$\widehat{AB}$的中点,过点C作CD的垂线,与DB的延长线相交于点E,若AC=3,BC=4,则DE=$\frac{35\sqrt{2}}{6}$.
如图,已知AB是⊙O的直径,点C在⊙O上,D是$\widehat{AB}$的中点,过点C作CD的垂线,与DB的延长线相交于点E,若AC=3,BC=4,则DE=$\frac{35\sqrt{2}}{6}$.