题目内容
20.若正整数x,y,z满足$\left\{\begin{array}{l}{x>y>z>663}\\{x+y+z=1998}\\{2x+3y+4z=5992}\end{array}\right.$,则(x,y,z)=(667,666,665).分析 先由②③得出y+2z=1996,借助y>z>663,求出z的值,再结合②求出x,y即可.
解答 解:$\left\{\begin{array}{l}{x>y>z>663①}\\{x+y+z=1998②}\\{2x+3y+4z=5992③}\end{array}\right.$,
③-②×2,得,y+2z=5992-1998×2=1996,
∵y>z>663,
∴3z<1996,
∴z<665$\frac{1}{3}$,
∵z>663,且为正整数,
∴z=664,或z=665;
∵y+2z=1996④,x+y+z=1998,
当z=664时,y=668,x=666(舍)
当z=665时,y=666,x=667;
故答案为:(667,666,665);
点评 此题是三元一次不定方程,主要考查了解字母细数的方程组的方法,不等式的性质,解本题的关键是得出y+2z=1996.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.计算2a-a的结果是( )
| A. | -2a | B. | 1 | C. | 2 | D. | a |
8. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )| A. | 2∠A=∠2-∠1 | B. | 3∠A=2(∠2-∠1) | C. | 3∠A=2∠1-∠2 | D. | ∠A=∠2-∠1 |
10.若b=$\sqrt{2-a}$+$\sqrt{2a-4}$+1,则a-3b+1的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
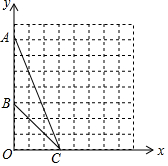 如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).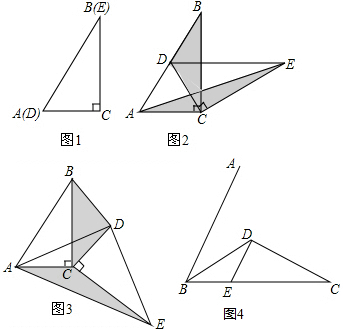
 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是( )
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是( ) 一次函数的图象经过点(-2,12)和(3,-3).
一次函数的图象经过点(-2,12)和(3,-3).