题目内容
11. 已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.
已知:如图,BE∥CF,BE、CF分别平分∠ABC和∠BCD.求证:AB∥CD.
分析 根据BE∥CF,得∠EBC=∠FCB,根据BE、CF分别平分∠ABC和∠BCD,得∠ABC=2∠EBC,∠BCD=2∠FCB,则∠ABC=∠BCD,根据内错角相等从而证明AB∥CD.
解答 证明:∵BE、CF分别平分∠ABC和∠BCD,
∴∠ABC=2∠EBC,∠BCD=2∠FCB,
∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC=∠BCD,
∴AB∥CD.
点评 本题考查了平行线的性质和判定以及角平分线的定义,解题时注意:内错角相等,两直线平行.

练习册系列答案
相关题目
19.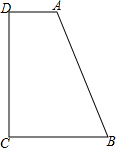 如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,AD=2,BC=4,如果在边DC上找一点P使得△PAD和△PBC相似,那么这样的点P存在的个数是( )
如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,AD=2,BC=4,如果在边DC上找一点P使得△PAD和△PBC相似,那么这样的点P存在的个数是( )
 如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,AD=2,BC=4,如果在边DC上找一点P使得△PAD和△PBC相似,那么这样的点P存在的个数是( )
如图,在梯形ABCD中,AD∥BC,∠D=90°,DC=6,AD=2,BC=4,如果在边DC上找一点P使得△PAD和△PBC相似,那么这样的点P存在的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列语句错误的是( )
| A. | 所有的实数都可用数轴上的点表示 | |
| B. | 无理数包括正无理数、零、负无理数 | |
| C. | 单项式中所有字母的指数的和叫做这个单项式的次数 | |
| D. | 两点之间线段最短 |
 如图,平行四边形ABCD的底AB=10,AB边上的高为3,AD=6,∠A=∠C=30°,求阴影部分的面积.
如图,平行四边形ABCD的底AB=10,AB边上的高为3,AD=6,∠A=∠C=30°,求阴影部分的面积.