题目内容
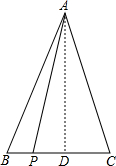 如图,在△ABC中,AB=AC=1,BC边上有2013个不同的点P1,P2,…P2013,记mi=APi2+BPi•PiC(i=1,2,…,2013),则m1+m2+…+m2013=
如图,在△ABC中,AB=AC=1,BC边上有2013个不同的点P1,P2,…P2013,记mi=APi2+BPi•PiC(i=1,2,…,2013),则m1+m2+…+m2013=考点:勾股定理,等腰三角形的性质
专题:规律型
分析:利用勾股定理求出APi2=AD2+PiD2,进一步推出APi2+BPi•PiC=1,解答即可.
解答:解:∵APi2=AD2+PiD2
=AD2+(BD-BPi)2
=AD2+BD2-2BD•BPi+BPi2
=1+BPi(BPi-BC)
=1-BPi•PiC,
∴APi2+BPi•PiC=1,
∴m1+m2+…+m2013=2013,
故答案为2013.
=AD2+(BD-BPi)2
=AD2+BD2-2BD•BPi+BPi2
=1+BPi(BPi-BC)
=1-BPi•PiC,
∴APi2+BPi•PiC=1,
∴m1+m2+…+m2013=2013,
故答案为2013.
点评:本题考查了勾股定理、等腰三角形的性质,根据题意,求出APi2+BPi•PiC=1是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
分式方程
-
=1的解是( )
| 1 |
| x-3 |
| 2x |
| 3-x |
| A、x=-4 | ||
| B、0 | ||
C、-
| ||
D、
|
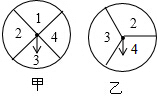 在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动甲、乙两个转盘,停止后指针所指的两个数字x,y分别表示两条线段的长,已知第三条线段的长为5,如果将转盘转动停止后得到的三条线段长记为(x,y,5).
在如图的甲、乙两个转盘中,指针指向每一个数字的机会是均等的,当同时转动甲、乙两个转盘,停止后指针所指的两个数字x,y分别表示两条线段的长,已知第三条线段的长为5,如果将转盘转动停止后得到的三条线段长记为(x,y,5). 如图,∠AOC,∠BOD都是直角;
如图,∠AOC,∠BOD都是直角;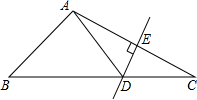 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为12cm,则△ABC的周长是
 如图,∠1=∠2=35°,则AB∥CD,理由是
如图,∠1=∠2=35°,则AB∥CD,理由是