题目内容
12. 如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE,若AB=1,∠AEB=15°,求AD的长度.
如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE,若AB=1,∠AEB=15°,求AD的长度.
分析 连接AC,由矩形性质可得∠E=∠DAE、BD=AC=CE,知∠E=∠CAE,由∠AEB=15°,则可得∠ADB=30°,进而可求出AD的长.
解答 解:连接AC,
∵四边形ABCD是矩形,
∴AD∥BE,AC=BD,且∠ADB=∠CAD=30°,
∴∠E=∠DAE,
又∵BD=CE,
∴CE=CA,
∴∠E=∠CAE,
∵∠CAD=∠CAE+∠DAE=30°,
∴∠ADB=30°,
∴BD=2AB=2,
∴AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{3}$.
点评 本题主要考查矩形性质以及勾股定理的运用,熟练掌握矩形对角线相等且互相平分、对边平行是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知23×42=2n,则n的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 有一块三角形土地,孪爷爷准备将这块土地分成面积相等的四块给他的四个儿子耕种,请你帮他制定出两种划分方案供他选择(画图说明).
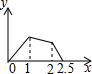
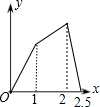
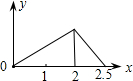
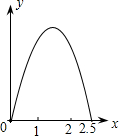
有一块三角形土地,孪爷爷准备将这块土地分成面积相等的四块给他的四个儿子耕种,请你帮他制定出两种划分方案供他选择(画图说明). 如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )
如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )