题目内容
如图,一副直角三角板△ABC和△DEF,已知BC=DF,∠F=30°,EF=2ED.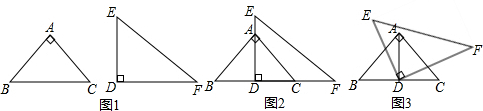
(1)直接写出∠B,∠C,∠E的度数;
(2)将△ABC和△DEF放置像图2的位置,点B、D、C、F在同一直线上,点A在DE上.
①△ABC固定不动,将三角板EDF绕点D逆时针旋转至EF∥CB(如图2),试求DF旋转的度数;并通过计算判断点A是否在EF上;
②在图3的位置上,△DEF绕点D继续逆时针旋转至DE与BC重合,在旋转过程中,两个三角形的边是否存在平行关系?若存在直接写出旋转的角度和平行关系,若不存在,请说明理由.

(1)直接写出∠B,∠C,∠E的度数;
(2)将△ABC和△DEF放置像图2的位置,点B、D、C、F在同一直线上,点A在DE上.
①△ABC固定不动,将三角板EDF绕点D逆时针旋转至EF∥CB(如图2),试求DF旋转的度数;并通过计算判断点A是否在EF上;
②在图3的位置上,△DEF绕点D继续逆时针旋转至DE与BC重合,在旋转过程中,两个三角形的边是否存在平行关系?若存在直接写出旋转的角度和平行关系,若不存在,请说明理由.
考点:几何变换综合题
专题:
分析:(1)根据三角形内角和定理和等腰三角形的性质得出即可;
(2)①求出∠B=∠C=∠DAC=∠DAB=45°,AD=
BC,延长DA交EF于H,则∠DHE=90°,根据三角形的内角和定理求出DH=
DF,推出DA=DH即可;②画出图形,根据平行线的判定得出即可.
(2)①求出∠B=∠C=∠DAC=∠DAB=45°,AD=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)如图1,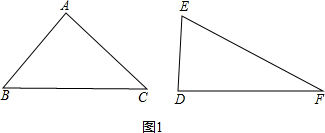
∠B=∠C=45°,∠E=60°;
(2)①如图2,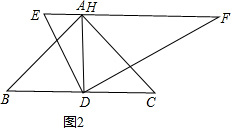
∵EF∥BC,
∴∠FDC=∠F=30°,
旋转的角度为30°,
∵△ABC是等腰直角三角形,AD⊥BC,
∴∠B=∠C=∠DAC=∠DAB=45°,AD=
BC,
延长DA交EF于H,则∠DHE=180°-(∠EDA+∠E)=90°,
∴DH⊥EF,
∵S△DEF=
ED•DF=
EF•DH,
∴DH=
DF,
∵BC=DF,
∴DA=DH,A与H重合,
∴点A在EF上.
②△DEF绕点D继续逆时针旋转至DE与BC重合,在旋转过程中,两个三角形的边存在平行关系,
当∠FDC=45°时,DE∥AC,AB∥DF,如图3,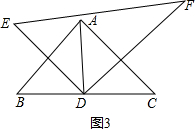
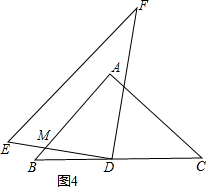
当∠FDC=75°时,EF∥AB,如图4,
∠EDB=180°-∠EDF-∠FDC=180°-90°-75°=15°,
∵∠B=45°,
∴∠AMD=15°+45°=60°,
∵∠E=60°,
∴∠E=∠AMD,
∴EF∥AB.

∠B=∠C=45°,∠E=60°;
(2)①如图2,

∵EF∥BC,
∴∠FDC=∠F=30°,
旋转的角度为30°,
∵△ABC是等腰直角三角形,AD⊥BC,
∴∠B=∠C=∠DAC=∠DAB=45°,AD=
| 1 |
| 2 |
延长DA交EF于H,则∠DHE=180°-(∠EDA+∠E)=90°,
∴DH⊥EF,
∵S△DEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴DH=
| 1 |
| 2 |
∵BC=DF,
∴DA=DH,A与H重合,
∴点A在EF上.
②△DEF绕点D继续逆时针旋转至DE与BC重合,在旋转过程中,两个三角形的边存在平行关系,
当∠FDC=45°时,DE∥AC,AB∥DF,如图3,

当∠FDC=75°时,EF∥AB,如图4,
∠EDB=180°-∠EDF-∠FDC=180°-90°-75°=15°,
∵∠B=45°,
∴∠AMD=15°+45°=60°,
∵∠E=60°,
∴∠E=∠AMD,
∴EF∥AB.

点评:本题考查了等腰三角形的性质,三角形的内角和定理,平行线的判定的应用,主要考查学生运用性质进行推理和计算的能力,题目比较好,难度偏大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
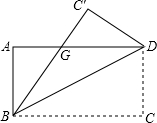 如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.
如图,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C落在点C′的位置,BC′交AD于点G.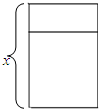 某校在新建学生宿舍时需如图所示的铝合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图).
某校在新建学生宿舍时需如图所示的铝合金窗框(别忘了中间还用了一根),它共用了长8米的铝合金,设长方形窗框的一边长为x米(如图). 如图,在△ABC中,CA=CB,O为外心,I为内心,D为BC上的点,且BI⊥DO.
如图,在△ABC中,CA=CB,O为外心,I为内心,D为BC上的点,且BI⊥DO. 如图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是
如图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是