题目内容
 如图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是
如图,已知△ABC中,∠B=90°,角平分线AD、CF相交于E,则∠AEC的度数是考点:三角形内角和定理
专题:
分析:根据三角形的内角和定理求出∠BAC+∠ACB,再根据角平分线的定义求出∠EAC+∠ECA,然后利用三角形的内角和定理列式计算即可得解.
解答:解:∵∠B=90°,
∴∠BAC+∠ACB=180°-90°=90°,
∵角平分线AD、CF相交于E,
∴∠EAC+∠ECA=
(∠BAC+∠ACB)=
×90°=45°,
在△ACE中,∠AEC=180°-(∠EAC+∠ECA)=180°-45°=135°.
故答案为:135°.
∴∠BAC+∠ACB=180°-90°=90°,
∵角平分线AD、CF相交于E,
∴∠EAC+∠ECA=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACE中,∠AEC=180°-(∠EAC+∠ECA)=180°-45°=135°.
故答案为:135°.
点评:本题考查了三角形的内角和定理,三角形的角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
相关题目
若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数y=
的图象上,则下列各式中,正确的是( )
| 1 |
| x |
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
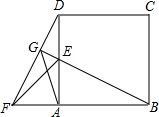 如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为
如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为