题目内容
 如图,Rt△ABC中,∠C=90°,∠A=30°,在AC边上取点O为圆心画圆,使⊙O经过A、B两点,下列结论:①AO=2CO;②AO=BC;③以O圆心,OC为半径的圆与AB相切;④延长BC交⊙O于D,则A、B、D是⊙O的三等分点.其中正确的序号是( )
如图,Rt△ABC中,∠C=90°,∠A=30°,在AC边上取点O为圆心画圆,使⊙O经过A、B两点,下列结论:①AO=2CO;②AO=BC;③以O圆心,OC为半径的圆与AB相切;④延长BC交⊙O于D,则A、B、D是⊙O的三等分点.其中正确的序号是( )| A、①②③④ | B、①②③ |
| C、②③④ | D、①③④ |
考点:切线的判定,含30度角的直角三角形
专题:
分析:连接OB,求出OA=OB和∠CBO=30°,根据含30度角的直角三角形性质求出OB=2OC,即可判断①、②;
过O作OD⊥AB于D,求出OD=OC,根据切线的判定即可判断③;
根据垂径定理求出DC=BC,求出AD=AB,得出等边三角形,即可判断④.
过O作OD⊥AB于D,求出OD=OC,根据切线的判定即可判断③;
根据垂径定理求出DC=BC,求出AD=AB,得出等边三角形,即可判断④.
解答:解:如图1,连接OB,

则OA=OB,
∵∠C=90°,∠A=30°,
∴∠ABO=∠A=30°,∠ABC=60°,
∴∠CBO=30°,
∴OB=2OC,
∴AO=2CO,∴①正确;
在Rt△OCB中,∠C=90°,OB>BC,
∵AO=OB,
∴AO>BC,∴②错误;
如图2,过O作OD⊥AB于D,

∵∠C=90°,∠ABO=∠CBO=30°,
∴OC=OD,
∴以O圆心,OC为半径的圆与AB相切,∴③正确;
如图3,连接AD,

∵∠ACB=90°,
∴根据垂径定理得:DC=BC,
∴AD=AB,
∵∠ABC=60°,
∴△ADB是等边三角形,
∴AD=AB=BD,
∴弧AD=弧AB=弧BD,
∴延长BC交⊙O于D,则A、B、D是⊙O的三等分点,∴④正确;
故选D.

则OA=OB,
∵∠C=90°,∠A=30°,
∴∠ABO=∠A=30°,∠ABC=60°,
∴∠CBO=30°,
∴OB=2OC,
∴AO=2CO,∴①正确;
在Rt△OCB中,∠C=90°,OB>BC,
∵AO=OB,
∴AO>BC,∴②错误;
如图2,过O作OD⊥AB于D,

∵∠C=90°,∠ABO=∠CBO=30°,
∴OC=OD,
∴以O圆心,OC为半径的圆与AB相切,∴③正确;
如图3,连接AD,

∵∠ACB=90°,
∴根据垂径定理得:DC=BC,
∴AD=AB,
∵∠ABC=60°,
∴△ADB是等边三角形,
∴AD=AB=BD,
∴弧AD=弧AB=弧BD,
∴延长BC交⊙O于D,则A、B、D是⊙O的三等分点,∴④正确;
故选D.
点评:本题考查了角平分线性质,含30度角的直角三角形性质,垂径定理,圆心角、弧、弦之间的关系,直角三角形的性质,等边三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度偏大.

练习册系列答案
相关题目
△ABC与△DEF的相似比为2:3,且△ABC的周长为10,则△DEF的周长是( )
| A、5 | B、10 | C、15 | D、20 |
 如图,已知矩形AOBC的面积为4,反比例函数y=
如图,已知矩形AOBC的面积为4,反比例函数y= 如图,方格纸中的每个小正方格都是边长为1的正方形,我们把以格点间连接为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,在建立平面直角坐标系后,点A的坐标为(1,1).
如图,方格纸中的每个小正方格都是边长为1的正方形,我们把以格点间连接为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,在建立平面直角坐标系后,点A的坐标为(1,1).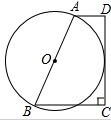 如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
如图,已知梯形ABCD中,AD∥BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.